Welcome to Subscribe On Youtube

1676. Lowest Common Ancestor of a Binary Tree IV

Description

Given the root of a binary tree and an array of TreeNode objects nodes, return the lowest common ancestor (LCA) of all the nodes in nodes. All the nodes will exist in the tree, and all values of the tree's nodes are unique.

Extending the definition of LCA on Wikipedia: "The lowest common ancestor of n nodes p1, p2, ..., pn in a binary tree T is the lowest node that has every pi as a descendant (where we allow a node to be a descendant of itself) for every valid i". A descendant of a node x is a node y that is on the path from node x to some leaf node.

 

Example 1:

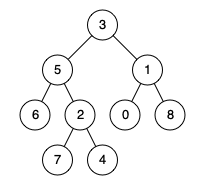
Input: root = [3,5,1,6,2,0,8,null,null,7,4], nodes = [4,7]
Output: 2
Explanation: The lowest common ancestor of nodes 4 and 7 is node 2.

Example 2:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], nodes = [1]
Output: 1
Explanation: The lowest common ancestor of a single node is the node itself.

Example 3:

Input: root = [3,5,1,6,2,0,8,null,null,7,4], nodes = [7,6,2,4]
Output: 5
Explanation: The lowest common ancestor of the nodes 7, 6, 2, and 4 is node 5.

 

Constraints:

• The number of nodes in the tree is in the range [1, 104].
• -109 <= Node.val <= 109
• All Node.val are unique.
• All nodes[i] will exist in the tree.
• All nodes[i] are distinct.

Solutions

• Java
• C++
• Python
• Javascript

• /**
   * Definition for a binary tree node.
   * public class TreeNode {
   *     int val;
   *     TreeNode left;
   *     TreeNode right;
   *     TreeNode(int x) { val = x; }
   * }
   */
  class Solution {
      private Set<Integer> s = new HashSet<>();
  
      public TreeNode lowestCommonAncestor(TreeNode root, TreeNode[] nodes) {
          for (TreeNode node : nodes) {
              s.add(node.val);
          }
          return dfs(root);
      }
  
      private TreeNode dfs(TreeNode root) {
          if (root == null || s.contains(root.val)) {
              return root;
          }
          TreeNode left = dfs(root.left);
          TreeNode right = dfs(root.right);
          if (left == null) {
              return right;
          }
          if (right == null) {
              return left;
          }
          return root;
      }
  }
  

• /**
   * Definition for a binary tree node.
   * struct TreeNode {
   *     int val;
   *     TreeNode *left;
   *     TreeNode *right;
   *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
   *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
   *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
   * };
   */
  class Solution {
  public:
      TreeNode* lowestCommonAncestor(TreeNode* root, vector<TreeNode*>& nodes) {
          unordered_set<int> s;
          for (auto node : nodes) s.insert(node->val);
          function<TreeNode*(TreeNode*)> dfs = [&](TreeNode* root) -> TreeNode* {
              if (!root || s.count(root->val)) return root;
              auto left = dfs(root->left);
              auto right = dfs(root->right);
              if (!left) return right;
              if (!right) return left;
              return root;
          };
          return dfs(root);
      }
  };
  

• # Definition for a binary tree node.
  # class TreeNode:
  #     def __init__(self, x):
  #         self.val = x
  #         self.left = None
  #         self.right = None
  
  
  class Solution:
      def lowestCommonAncestor(
          self, root: 'TreeNode', nodes: 'List[TreeNode]'
      ) -> 'TreeNode':
          def dfs(root):
              if root is None or root.val in s:
                  return root
              left, right = dfs(root.left), dfs(root.right)
              if left and right:
                  return root
              return left or right
  
          s = {node.val for node in nodes}
          return dfs(root)
  
  

• /**
   * Definition for a binary tree node.
   * function TreeNode(val) {
   *     this.val = val;
   *     this.left = this.right = null;
   * }
   */
  /**
   * @param {TreeNode} root
   * @param {TreeNode[]} nodes
   * @return {TreeNode}
   */
  var lowestCommonAncestor = function (root, nodes) {
      const s = new Set();
      for (const node of nodes) {
          s.add(node.val);
      }
      function dfs(root) {
          if (!root || s.has(root.val)) {
              return root;
          }
          const [left, right] = [dfs(root.left), dfs(root.right)];
          if (left && right) {
              return root;
          }
          return left || right;
      }
      return dfs(root);
  };
  
  

All Problems

All Solutions