1627. Graph Connectivity With Threshold

Description

We have n cities labeled from 1 to n. Two different cities with labels x and y are directly connected by a bidirectional road if and only if x and y share a common divisor strictly greater than some threshold. More formally, cities with labels x and y have a road between them if there exists an integer z such that all of the following are true:

x % z == 0,
y % z == 0, and
z > threshold.

Given the two integers, n and threshold, and an array of queries, you must determine for each queries[i] = [a_i, b_i] if cities a_i and b_i are connected directly or indirectly. (i.e. there is some path between them).

Return an array answer, where answer.length == queries.length and answer[i] is true if for the i^th query, there is a path between a_i and b_i, or answer[i] is false if there is no path.

Example 1:

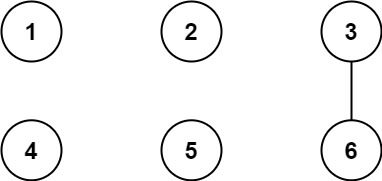
Input: n = 6, threshold = 2, queries = [[1,4],[2,5],[3,6]]
Output: [false,false,true]
Explanation: The divisors for each number:
1:   1
2:   1, 2
3:   1, 3
4:   1, 2, 4
5:   1, 5
6:   1, 2, 3, 6
Using the underlined divisors above the threshold, only cities 3 and 6 share a common divisor, so they are the
only ones directly connected. The result of each query:
[1,4]   1 is not connected to 4
[2,5]   2 is not connected to 5
[3,6]   3 is connected to 6 through path 3--6

Example 2:

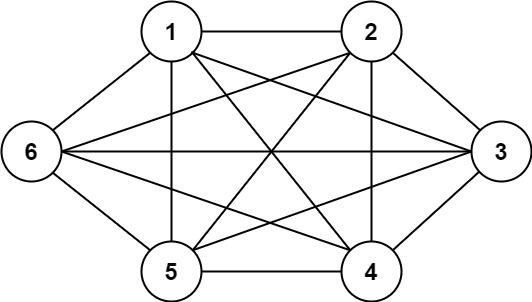
Input: n = 6, threshold = 0, queries = [[4,5],[3,4],[3,2],[2,6],[1,3]]
Output: [true,true,true,true,true]
Explanation: The divisors for each number are the same as the previous example. However, since the threshold is 0,
all divisors can be used. Since all numbers share 1 as a divisor, all cities are connected.

Example 3:

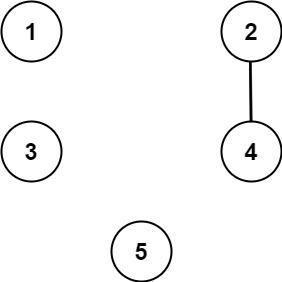
Input: n = 5, threshold = 1, queries = [[4,5],[4,5],[3,2],[2,3],[3,4]]
Output: [false,false,false,false,false]
Explanation: Only cities 2 and 4 share a common divisor 2 which is strictly greater than the threshold 1, so they are the only ones directly connected.
Please notice that there can be multiple queries for the same pair of nodes [x, y], and that the query [x, y] is equivalent to the query [y, x].

Constraints:

2 <= n <= 10⁴
0 <= threshold <= n
1 <= queries.length <= 10⁵
queries[i].length == 2
1 <= a_i, b_i <= cities
a_i != b_i

Solutions

Solution 1: Union-Find

We can enumerate $z$ and its multiples, and use union-find to connect them. In this way, for each query $[a, b]$, we only need to determine whether $a$ and $b$ are in the same connected component.

The time complexity is $O(n \times \log n \times (\alpha(n) + q))$, and the space complexity is $O(n)$. Here, $n$ and $q$ are the number of nodes and queries, respectively, and $\alpha$ is the inverse function of the Ackermann function.

class UnionFind {
    private int[] p;
    private int[] size;

    public UnionFind(int n) {
        p = new int[n];
        size = new int[n];
        for (int i = 0; i < n; ++i) {
            p[i] = i;
            size[i] = 1;
        }
    }

    public int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }

    public boolean union(int a, int b) {
        int pa = find(a), pb = find(b);
        if (pa == pb) {
            return false;
        }
        if (size[pa] > size[pb]) {
            p[pb] = pa;
            size[pa] += size[pb];
        } else {
            p[pa] = pb;
            size[pb] += size[pa];
        }
        return true;
    }
}

class Solution {
    public List<Boolean> areConnected(int n, int threshold, int[][] queries) {
        UnionFind uf = new UnionFind(n + 1);
        for (int a = threshold + 1; a <= n; ++a) {
            for (int b = a + a; b <= n; b += a) {
                uf.union(a, b);
            }
        }
        List<Boolean> ans = new ArrayList<>();
        for (var q : queries) {
            ans.add(uf.find(q[0]) == uf.find(q[1]));
        }
        return ans;
    }
}

class UnionFind {
public:
    UnionFind(int n) {
        p = vector<int>(n);
        size = vector<int>(n, 1);
        iota(p.begin(), p.end(), 0);
    }

    bool unite(int a, int b) {
        int pa = find(a), pb = find(b);
        if (pa == pb) {
            return false;
        }
        if (size[pa] > size[pb]) {
            p[pb] = pa;
            size[pa] += size[pb];
        } else {
            p[pa] = pb;
            size[pb] += size[pa];
        }
        return true;
    }

    int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }

private:
    vector<int> p, size;
};

class Solution {
public:
    vector<bool> areConnected(int n, int threshold, vector<vector<int>>& queries) {
        UnionFind uf(n + 1);
        for (int a = threshold + 1; a <= n; ++a) {
            for (int b = a + a; b <= n; b += a) {
                uf.unite(a, b);
            }
        }
        vector<bool> ans;
        for (auto& q : queries) {
            ans.push_back(uf.find(q[0]) == uf.find(q[1]));
        }
        return ans;
    }
};

class UnionFind:
    def __init__(self, n):
        self.p = list(range(n))
        self.size = [1] * n

    def find(self, x):
        if self.p[x] != x:
            self.p[x] = self.find(self.p[x])
        return self.p[x]

    def union(self, a, b):
        pa, pb = self.find(a), self.find(b)
        if pa == pb:
            return False
        if self.size[pa] > self.size[pb]:
            self.p[pb] = pa
            self.size[pa] += self.size[pb]
        else:
            self.p[pa] = pb
            self.size[pb] += self.size[pa]
        return True


class Solution:
    def areConnected(
        self, n: int, threshold: int, queries: List[List[int]]
    ) -> List[bool]:
        uf = UnionFind(n + 1)
        for a in range(threshold + 1, n + 1):
            for b in range(a + a, n + 1, a):
                uf.union(a, b)
        return [uf.find(a) == uf.find(b) for a, b in queries]

type unionFind struct {
	p, size []int
}

func newUnionFind(n int) *unionFind {
	p := make([]int, n)
	size := make([]int, n)
	for i := range p {
		p[i] = i
		size[i] = 1
	}
	return &unionFind{p, size}
}

func (uf *unionFind) find(x int) int {
	if uf.p[x] != x {
		uf.p[x] = uf.find(uf.p[x])
	}
	return uf.p[x]
}

func (uf *unionFind) union(a, b int) bool {
	pa, pb := uf.find(a), uf.find(b)
	if pa == pb {
		return false
	}
	if uf.size[pa] > uf.size[pb] {
		uf.p[pb] = pa
		uf.size[pa] += uf.size[pb]
	} else {
		uf.p[pa] = pb
		uf.size[pb] += uf.size[pa]
	}
	return true
}

func areConnected(n int, threshold int, queries [][]int) []bool {
	uf := newUnionFind(n + 1)
	for a := threshold + 1; a <= n; a++ {
		for b := a + a; b <= n; b += a {
			uf.union(a, b)
		}
	}
	ans := make([]bool, len(queries))
	for i, q := range queries {
		ans[i] = uf.find(q[0]) == uf.find(q[1])
	}
	return ans
}

class UnionFind {
    p: number[];
    size: number[];
    constructor(n: number) {
        this.p = Array(n)
            .fill(0)
            .map((_, i) => i);
        this.size = Array(n).fill(1);
    }

    find(x: number): number {
        if (this.p[x] !== x) {
            this.p[x] = this.find(this.p[x]);
        }
        return this.p[x];
    }

    union(a: number, b: number): boolean {
        const [pa, pb] = [this.find(a), this.find(b)];
        if (pa === pb) {
            return false;
        }
        if (this.size[pa] > this.size[pb]) {
            this.p[pb] = pa;
            this.size[pa] += this.size[pb];
        } else {
            this.p[pa] = pb;
            this.size[pb] += this.size[pa];
        }
        return true;
    }
}

function areConnected(n: number, threshold: number, queries: number[][]): boolean[] {
    const uf = new UnionFind(n + 1);
    for (let a = threshold + 1; a <= n; ++a) {
        for (let b = a * 2; b <= n; b += a) {
            uf.union(a, b);
        }
    }
    return queries.map(([a, b]) => uf.find(a) === uf.find(b));
}

1627 - Graph Connectivity With Threshold

1627. Graph Connectivity With Threshold

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

1627. Graph Connectivity With Threshold

Description

Solutions

All Problems

All Solutions