Welcome to Subscribe On Youtube
1617. Count Subtrees With Max Distance Between Cities
Description
There are n cities numbered from 1 to n. You are given an array edges of size n-1, where edges[i] = [ui, vi] represents a bidirectional edge between cities ui and vi. There exists a unique path between each pair of cities. In other words, the cities form a tree.
A subtree is a subset of cities where every city is reachable from every other city in the subset, where the path between each pair passes through only the cities from the subset. Two subtrees are different if there is a city in one subtree that is not present in the other.
For each d from 1 to n-1, find the number of subtrees in which the maximum distance between any two cities in the subtree is equal to d.
Return an array of size n-1 where the dth element (1-indexed) is the number of subtrees in which the maximum distance between any two cities is equal to d.
Notice that the distance between the two cities is the number of edges in the path between them.
Example 1:
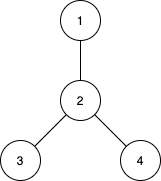
Input: n = 4, edges = [[1,2],[2,3],[2,4]]
Output: [3,4,0]
Explanation:
The subtrees with subsets {1,2}, {2,3} and {2,4} have a max distance of 1.
The subtrees with subsets {1,2,3}, {1,2,4}, {2,3,4} and {1,2,3,4} have a max distance of 2.
No subtree has two nodes where the max distance between them is 3.
Example 2:
Input: n = 2, edges = [[1,2]] Output: [1]
Example 3:
Input: n = 3, edges = [[1,2],[2,3]] Output: [2,1]
Constraints:
2 <= n <= 15edges.length == n-1edges[i].length == 21 <= ui, vi <= n- All pairs
(ui, vi)are distinct.
Solutions
Solution 1: Depth-First Search + Hash Table
We noticed $n \leq 15$, so we can consider using binary enumeration to enumerate all subtrees. The maximum distance between nodes in a subtree is actually the longest path between two nodes in the subtree, which is the diameter of the tree. To solve the diameter of the tree, you can generally use DFS or BFS. First find one endpoint of the tree diameter, and then start from that endpoint to find the other endpoint of the tree. The length of the path between these two endpoints is the diameter of the tree.
Next, we describe the specific code implementation in detail.
We first construct the adjacency table $g$ based on the array $edges$, where $g[u]$ represents all adjacent nodes of the node $u$.
Use a binary number $mask$ to represent the subtree, where the $i$ bit of $mask$ is $1$, which means that the node $i$ is in the subtree, otherwise it means that the node $i$ is not in the subtree. Each node has two states, in the subtree or not in the subtree. There are $n$ nodes, so there are $2^n$ states in total.
Next, we enumerate the subtrees $mask$ in the range $[1,..2^n-1]$, for each subtree:
If only one binary bit in the binary representation of $mask$ is $1$, that is, $mask \in [1,2,4,8,\cdots,2^{n-1}]$, skip the $mask$, because the subtrees represented by these $mask$ have only one node, which does not meet the meaning of the question;
Otherwise, we find the position where the highest binary bit in the binary representation of $mask$ is $1$, denoted as $cur$. Then starting from the node $cur$, we find an endpoint of the tree diameter $nxt$ through depth-first search or breadth-first search. Then we start from the node $nxt$, also through depth-first search or breadth-first search, and record the maximum distance $mx$ in the process.
When you reach the deepest node, you can know the diameter of the tree. At this time we update the answer array $ans$ and add $1$ to the value of $ans[mx-1]$. Note that this is $mx-1$, because the maximum distance in the question is counted from $1$.
Finally, after enumerating all subtrees, return the answer array $ans$.
Time complexity $O(2^n \times n)$, space complexity $O(n)$. Among them, $n$ is the number of nodes.
Solution 2
This implementation uses breadth-first search, followed by hash table, followed by bit manipulation. It traverses the relevant values and updates its state as each value is processed. A keyed container records values that must be found or updated efficiently. The auxiliary container determines which pending state is processed next.
-
class Solution { private List<Integer>[] g; private int msk; private int nxt; private int mx; public int[] countSubgraphsForEachDiameter(int n, int[][] edges) { g = new List[n]; Arrays.setAll(g, k -> new ArrayList<>()); for (int[] e : edges) { int u = e[0] - 1, v = e[1] - 1; g[u].add(v); g[v].add(u); } int[] ans = new int[n - 1]; for (int mask = 1; mask < 1 << n; ++mask) { if ((mask & (mask - 1)) == 0) { continue; } msk = mask; mx = 0; int cur = 31 - Integer.numberOfLeadingZeros(msk); dfs(cur, 0); if (msk == 0) { msk = mask; mx = 0; dfs(nxt, 0); ++ans[mx - 1]; } } return ans; } private void dfs(int u, int d) { msk ^= 1 << u; if (mx < d) { mx = d; nxt = u; } for (int v : g[u]) { if ((msk >> v & 1) == 1) { dfs(v, d + 1); } } } } // Solution 2 class Solution { private List<Integer>[] g; private int msk; private int nxt; public int[] countSubgraphsForEachDiameter(int n, int[][] edges) { g = new List[n]; Arrays.setAll(g, k -> new ArrayList<>()); for (int[] e : edges) { int u = e[0] - 1, v = e[1] - 1; g[u].add(v); g[v].add(u); } int[] ans = new int[n - 1]; for (int mask = 1; mask < 1 << n; ++mask) { if ((mask & (mask - 1)) == 0) { continue; } msk = mask; int cur = 31 - Integer.numberOfLeadingZeros(msk); bfs(cur); if (msk == 0) { msk = mask; int mx = bfs(nxt); ++ans[mx - 1]; } } return ans; } private int bfs(int u) { int d = -1; Deque<Integer> q = new ArrayDeque<>(); q.offer(u); msk ^= 1 << u; while (!q.isEmpty()) { ++d; for (int k = q.size(); k > 0; --k) { u = q.poll(); nxt = u; for (int v : g[u]) { if ((msk >> v & 1) == 1) { msk ^= 1 << v; q.offer(v); } } } } return d; } } -
class Solution { public: vector<int> countSubgraphsForEachDiameter(int n, vector<vector<int>>& edges) { vector<vector<int>> g(n); for (auto& e : edges) { int u = e[0] - 1, v = e[1] - 1; g[u].emplace_back(v); g[v].emplace_back(u); } vector<int> ans(n - 1); int nxt = 0, msk = 0, mx = 0; function<void(int, int)> dfs = [&](int u, int d) { msk ^= 1 << u; if (mx < d) { mx = d; nxt = u; } for (int& v : g[u]) { if (msk >> v & 1) { dfs(v, d + 1); } } }; for (int mask = 1; mask < 1 << n; ++mask) { if ((mask & (mask - 1)) == 0) { continue; } msk = mask; mx = 0; int cur = 31 - __builtin_clz(msk); dfs(cur, 0); if (msk == 0) { msk = mask; mx = 0; dfs(nxt, 0); ++ans[mx - 1]; } } return ans; } }; // Solution 2 class Solution { public: vector<int> countSubgraphsForEachDiameter(int n, vector<vector<int>>& edges) { vector<vector<int>> g(n); for (auto& e : edges) { int u = e[0] - 1, v = e[1] - 1; g[u].emplace_back(v); g[v].emplace_back(u); } vector<int> ans(n - 1); int nxt = 0, msk = 0; auto bfs = [&](int u) -> int { int d = -1; msk ^= 1 << u; queue<int> q{{u}}; while (!q.empty()) { ++d; for (int k = q.size(); k; --k) { u = q.front(); nxt = u; q.pop(); for (int& v : g[u]) { if (msk >> v & 1) { msk ^= 1 << v; q.push(v); } } } } return d; }; for (int mask = 1; mask < 1 << n; ++mask) { if ((mask & (mask - 1)) == 0) { continue; } msk = mask; int cur = 31 - __builtin_clz(msk); bfs(cur); if (msk == 0) { msk = mask; int mx = bfs(nxt); ++ans[mx - 1]; } } return ans; } }; -
class Solution: def countSubgraphsForEachDiameter( self, n: int, edges: List[List[int]] ) -> List[int]: def dfs(u: int, d: int = 0): nonlocal mx, nxt, msk if mx < d: mx, nxt = d, u msk ^= 1 << u for v in g[u]: if msk >> v & 1: dfs(v, d + 1) g = defaultdict(list) for u, v in edges: u, v = u - 1, v - 1 g[u].append(v) g[v].append(u) ans = [0] * (n - 1) nxt = mx = 0 for mask in range(1, 1 << n): if mask & (mask - 1) == 0: continue msk, mx = mask, 0 cur = msk.bit_length() - 1 dfs(cur) if msk == 0: msk, mx = mask, 0 dfs(nxt) ans[mx - 1] += 1 return ans # Solution 2 class Solution: def countSubgraphsForEachDiameter( self, n: int, edges: List[List[int]] ) -> List[int]: def bfs(u: int) -> int: d = -1 q = deque([u]) nonlocal msk, nxt msk ^= 1 << u while q: d += 1 for _ in range(len(q)): nxt = u = q.popleft() for v in g[u]: if msk >> v & 1: msk ^= 1 << v q.append(v) return d g = defaultdict(list) for u, v in edges: u, v = u - 1, v - 1 g[u].append(v) g[v].append(u) ans = [0] * (n - 1) nxt = 0 for mask in range(1, 1 << n): if mask & (mask - 1) == 0: continue msk = mask cur = msk.bit_length() - 1 bfs(cur) if msk == 0: msk = mask mx = bfs(nxt) ans[mx - 1] += 1 return ans -
func countSubgraphsForEachDiameter(n int, edges [][]int) []int { g := make([][]int, n) for _, e := range edges { u, v := e[0]-1, e[1]-1 g[u] = append(g[u], v) g[v] = append(g[v], u) } ans := make([]int, n-1) var msk, nxt, mx int var dfs func(int, int) dfs = func(u, d int) { msk ^= 1 << u if mx < d { mx, nxt = d, u } for _, v := range g[u] { if msk>>v&1 == 1 { dfs(v, d+1) } } } for mask := 1; mask < 1<<n; mask++ { if mask&(mask-1) == 0 { continue } msk, mx = mask, 0 cur := bits.Len(uint(msk)) - 1 dfs(cur, 0) if msk == 0 { msk, mx = mask, 0 dfs(nxt, 0) ans[mx-1]++ } } return ans } // Solution 2 func countSubgraphsForEachDiameter(n int, edges [][]int) []int { g := make([][]int, n) for _, e := range edges { u, v := e[0]-1, e[1]-1 g[u] = append(g[u], v) g[v] = append(g[v], u) } ans := make([]int, n-1) var msk, nxt int bfs := func(u int) int { d := -1 q := []int{u} msk ^= 1 << u for len(q) > 0 { d++ for k := len(q); k > 0; k-- { u = q[0] q = q[1:] nxt = u for _, v := range g[u] { if msk>>v&1 == 1 { msk ^= 1 << v q = append(q, v) } } } } return d } for mask := 1; mask < 1<<n; mask++ { if mask&(mask-1) == 0 { continue } msk = mask cur := bits.Len(uint(msk)) - 1 bfs(cur) if msk == 0 { msk = mask mx := bfs(nxt) ans[mx-1]++ } } return ans } -
function countSubgraphsForEachDiameter(n: number, edges: number[][]): number[] { const g = Array.from({ length: n }, () => []); for (const [u, v] of edges) { g[u - 1].push(v - 1); g[v - 1].push(u - 1); } const ans: number[] = new Array(n - 1).fill(0); let [mx, msk, nxt] = [0, 0, 0]; const dfs = (u: number, d: number) => { if (mx < d) { mx = d; nxt = u; } msk ^= 1 << u; for (const v of g[u]) { if ((msk >> v) & 1) { dfs(v, d + 1); } } }; for (let mask = 1; mask < 1 << n; ++mask) { if ((mask & (mask - 1)) === 0) { continue; } msk = mask; mx = 0; const cur = 31 - numberOfLeadingZeros(msk); dfs(cur, 0); if (msk === 0) { msk = mask; mx = 0; dfs(nxt, 0); ++ans[mx - 1]; } } return ans; } function numberOfLeadingZeros(i: number): number { if (i == 0) return 32; let n = 1; if (i >>> 16 == 0) { n += 16; i <<= 16; } if (i >>> 24 == 0) { n += 8; i <<= 8; } if (i >>> 28 == 0) { n += 4; i <<= 4; } if (i >>> 30 == 0) { n += 2; i <<= 2; } n -= i >>> 31; return n; } // Solution 2 function countSubgraphsForEachDiameter(n: number, edges: number[][]): number[] { const g = Array.from({ length: n }, () => []); for (const [u, v] of edges) { g[u - 1].push(v - 1); g[v - 1].push(u - 1); } const ans: number[] = new Array(n - 1).fill(0); let [msk, nxt] = [0, 0]; const bfs = (u: number) => { let d = -1; const q = [u]; msk ^= 1 << u; while (q.length) { ++d; for (let k = q.length; k; --k) { u = q.shift()!; nxt = u; for (const v of g[u]) { if ((msk >> v) & 1) { msk ^= 1 << v; q.push(v); } } } } return d; }; for (let mask = 1; mask < 1 << n; ++mask) { if ((mask & (mask - 1)) === 0) { continue; } msk = mask; const cur = 31 - numberOfLeadingZeros(msk); bfs(cur); if (msk === 0) { msk = mask; const mx = bfs(nxt); ++ans[mx - 1]; } } return ans; } function numberOfLeadingZeros(i: number): number { if (i == 0) return 32; let n = 1; if (i >>> 16 == 0) { n += 16; i <<= 16; } if (i >>> 24 == 0) { n += 8; i <<= 8; } if (i >>> 28 == 0) { n += 4; i <<= 4; } if (i >>> 30 == 0) { n += 2; i <<= 2; } n -= i >>> 31; return n; } -
class Solution { private List<Integer>[] g; private int msk; private int nxt; public int[] countSubgraphsForEachDiameter(int n, int[][] edges) { g = new List[n]; Arrays.setAll(g, k -> new ArrayList<>()); for (int[] e : edges) { int u = e[0] - 1, v = e[1] - 1; g[u].add(v); g[v].add(u); } int[] ans = new int[n - 1]; for (int mask = 1; mask < 1 << n; ++mask) { if ((mask & (mask - 1)) == 0) { continue; } msk = mask; int cur = 31 - Integer.numberOfLeadingZeros(msk); bfs(cur); if (msk == 0) { msk = mask; int mx = bfs(nxt); ++ans[mx - 1]; } } return ans; } private int bfs(int u) { int d = -1; Deque<Integer> q = new ArrayDeque<>(); q.offer(u); msk ^= 1 << u; while (!q.isEmpty()) { ++d; for (int k = q.size(); k > 0; --k) { u = q.poll(); nxt = u; for (int v : g[u]) { if ((msk >> v & 1) == 1) { msk ^= 1 << v; q.offer(v); } } } } return d; } } -
class Solution { public: vector<int> countSubgraphsForEachDiameter(int n, vector<vector<int>>& edges) { vector<vector<int>> g(n); for (auto& e : edges) { int u = e[0] - 1, v = e[1] - 1; g[u].emplace_back(v); g[v].emplace_back(u); } vector<int> ans(n - 1); int nxt = 0, msk = 0; auto bfs = [&](int u) -> int { int d = -1; msk ^= 1 << u; queue<int> q{{u}}; while (!q.empty()) { ++d; for (int k = q.size(); k; --k) { u = q.front(); nxt = u; q.pop(); for (int& v : g[u]) { if (msk >> v & 1) { msk ^= 1 << v; q.push(v); } } } } return d; }; for (int mask = 1; mask < 1 << n; ++mask) { if ((mask & (mask - 1)) == 0) { continue; } msk = mask; int cur = 31 - __builtin_clz(msk); bfs(cur); if (msk == 0) { msk = mask; int mx = bfs(nxt); ++ans[mx - 1]; } } return ans; } }; -
class Solution: def countSubgraphsForEachDiameter( self, n: int, edges: List[List[int]] ) -> List[int]: def bfs(u: int) -> int: d = -1 q = deque([u]) nonlocal msk, nxt msk ^= 1 << u while q: d += 1 for _ in range(len(q)): nxt = u = q.popleft() for v in g[u]: if msk >> v & 1: msk ^= 1 << v q.append(v) return d g = defaultdict(list) for u, v in edges: u, v = u - 1, v - 1 g[u].append(v) g[v].append(u) ans = [0] * (n - 1) nxt = 0 for mask in range(1, 1 << n): if mask & (mask - 1) == 0: continue msk = mask cur = msk.bit_length() - 1 bfs(cur) if msk == 0: msk = mask mx = bfs(nxt) ans[mx - 1] += 1 return ans -
func countSubgraphsForEachDiameter(n int, edges [][]int) []int { g := make([][]int, n) for _, e := range edges { u, v := e[0]-1, e[1]-1 g[u] = append(g[u], v) g[v] = append(g[v], u) } ans := make([]int, n-1) var msk, nxt int bfs := func(u int) int { d := -1 q := []int{u} msk ^= 1 << u for len(q) > 0 { d++ for k := len(q); k > 0; k-- { u = q[0] q = q[1:] nxt = u for _, v := range g[u] { if msk>>v&1 == 1 { msk ^= 1 << v q = append(q, v) } } } } return d } for mask := 1; mask < 1<<n; mask++ { if mask&(mask-1) == 0 { continue } msk = mask cur := bits.Len(uint(msk)) - 1 bfs(cur) if msk == 0 { msk = mask mx := bfs(nxt) ans[mx-1]++ } } return ans } -
function countSubgraphsForEachDiameter(n: number, edges: number[][]): number[] { const g = Array.from({ length: n }, () => []); for (const [u, v] of edges) { g[u - 1].push(v - 1); g[v - 1].push(u - 1); } const ans: number[] = new Array(n - 1).fill(0); let [msk, nxt] = [0, 0]; const bfs = (u: number) => { let d = -1; const q = [u]; msk ^= 1 << u; while (q.length) { ++d; for (let k = q.length; k; --k) { u = q.shift()!; nxt = u; for (const v of g[u]) { if ((msk >> v) & 1) { msk ^= 1 << v; q.push(v); } } } } return d; }; for (let mask = 1; mask < 1 << n; ++mask) { if ((mask & (mask - 1)) === 0) { continue; } msk = mask; const cur = 31 - numberOfLeadingZeros(msk); bfs(cur); if (msk === 0) { msk = mask; const mx = bfs(nxt); ++ans[mx - 1]; } } return ans; } function numberOfLeadingZeros(i: number): number { if (i == 0) return 32; let n = 1; if (i >>> 16 == 0) { n += 16; i <<= 16; } if (i >>> 24 == 0) { n += 8; i <<= 8; } if (i >>> 28 == 0) { n += 4; i <<= 4; } if (i >>> 30 == 0) { n += 2; i <<= 2; } n -= i >>> 31; return n; }