Welcome to Subscribe On Youtube
1615. Maximal Network Rank
Description
There is an infrastructure of n cities with some number of roads connecting these cities. Each roads[i] = [ai, bi] indicates that there is a bidirectional road between cities ai and bi.
The network rank of two different cities is defined as the total number of directly connected roads to either city. If a road is directly connected to both cities, it is only counted once.
The maximal network rank of the infrastructure is the maximum network rank of all pairs of different cities.
Given the integer n and the array roads, return the maximal network rank of the entire infrastructure.
Example 1:
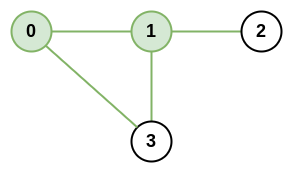
Input: n = 4, roads = [[0,1],[0,3],[1,2],[1,3]] Output: 4 Explanation: The network rank of cities 0 and 1 is 4 as there are 4 roads that are connected to either 0 or 1. The road between 0 and 1 is only counted once.
Example 2:
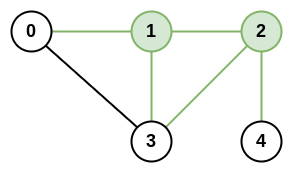
Input: n = 5, roads = [[0,1],[0,3],[1,2],[1,3],[2,3],[2,4]] Output: 5 Explanation: There are 5 roads that are connected to cities 1 or 2.
Example 3:
Input: n = 8, roads = [[0,1],[1,2],[2,3],[2,4],[5,6],[5,7]] Output: 5 Explanation: The network rank of 2 and 5 is 5. Notice that all the cities do not have to be connected.
Constraints:
2 <= n <= 1000 <= roads.length <= n * (n - 1) / 2roads[i].length == 20 <= ai, bi <= n-1ai != bi- Each pair of cities has at most one road connecting them.
Solutions
-
class Solution { public int maximalNetworkRank(int n, int[][] roads) { int[][] g = new int[n][n]; int[] cnt = new int[n]; for (var r : roads) { int a = r[0], b = r[1]; g[a][b] = 1; g[b][a] = 1; ++cnt[a]; ++cnt[b]; } int ans = 0; for (int a = 0; a < n; ++a) { for (int b = a + 1; b < n; ++b) { ans = Math.max(ans, cnt[a] + cnt[b] - g[a][b]); } } return ans; } } -
class Solution { public: int maximalNetworkRank(int n, vector<vector<int>>& roads) { int cnt[n]; int g[n][n]; memset(cnt, 0, sizeof(cnt)); memset(g, 0, sizeof(g)); for (auto& r : roads) { int a = r[0], b = r[1]; g[a][b] = g[b][a] = 1; ++cnt[a]; ++cnt[b]; } int ans = 0; for (int a = 0; a < n; ++a) { for (int b = a + 1; b < n; ++b) { ans = max(ans, cnt[a] + cnt[b] - g[a][b]); } } return ans; } }; -
class Solution: def maximalNetworkRank(self, n: int, roads: List[List[int]]) -> int: g = defaultdict(set) for a, b in roads: g[a].add(b) g[b].add(a) ans = 0 for a in range(n): for b in range(a + 1, n): if (t := len(g[a]) + len(g[b]) - (a in g[b])) > ans: ans = t return ans -
func maximalNetworkRank(n int, roads [][]int) (ans int) { g := make([][]int, n) cnt := make([]int, n) for i := range g { g[i] = make([]int, n) } for _, r := range roads { a, b := r[0], r[1] g[a][b], g[b][a] = 1, 1 cnt[a]++ cnt[b]++ } for a := 0; a < n; a++ { for b := a + 1; b < n; b++ { ans = max(ans, cnt[a]+cnt[b]-g[a][b]) } } return } -
function maximalNetworkRank(n: number, roads: number[][]): number { const g: number[][] = Array.from(new Array(n), () => new Array(n).fill(0)); const cnt: number[] = new Array(n).fill(0); for (const [a, b] of roads) { g[a][b] = 1; g[b][a] = 1; ++cnt[a]; ++cnt[b]; } let ans = 0; for (let a = 0; a < n; ++a) { for (let b = a + 1; b < n; ++b) { ans = Math.max(ans, cnt[a] + cnt[b] - g[a][b]); } } return ans; }