Welcome to Subscribe On Youtube
1612. Check If Two Expression Trees are Equivalent
Description
A binary expression tree is a kind of binary tree used to represent arithmetic expressions. Each node of a binary expression tree has either zero or two children. Leaf nodes (nodes with 0 children) correspond to operands (variables), and internal nodes (nodes with two children) correspond to the operators. In this problem, we only consider the '+' operator (i.e. addition).
You are given the roots of two binary expression trees, root1 and root2. Return true if the two binary expression trees are equivalent. Otherwise, return false.
Two binary expression trees are equivalent if they evaluate to the same value regardless of what the variables are set to.
Example 1:
Input: root1 = [x], root2 = [x] Output: true
Example 2:
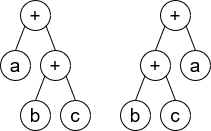
Input: root1 = [+,a,+,null,null,b,c], root2 = [+,+,a,b,c]
Output: true
Explanation: a + (b + c) == (b + c) + a
Example 3:
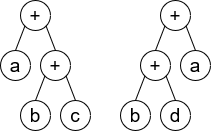
Input: root1 = [+,a,+,null,null,b,c], root2 = [+,+,a,b,d]
Output: false
Explanation: a + (b + c) != (b + d) + a
Constraints:
- The number of nodes in both trees are equal, odd and, in the range
[1, 4999]. Node.valis'+'or a lower-case English letter.- It's guaranteed that the tree given is a valid binary expression tree.
Follow up: What will you change in your solution if the tree also supports the '-' operator (i.e. subtraction)?
Solutions
Just count the type and number of letters in the two expression trees. Because it’s + only, (a+b)+c is same as a+(b+c)
Follow up question
What will you change in your solution if the tree also supports the ‘-‘ operator (i.e. subtraction). Then use 2 maps, one for + records, and one for - records.
-
/** * Definition for a binary tree node. * class Node { * char val; * Node left; * Node right; * Node() {this.val = ' ';} * Node(char val) { this.val = val; } * Node(char val, Node left, Node right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { private int[] cnt = new int[26]; public boolean checkEquivalence(Node root1, Node root2) { dfs(root1, 1); dfs(root2, -1); for (int x : cnt) { if (x != 0) { return false; } } return true; } private void dfs(Node root, int v) { if (root == null) { return; } if (root.val != '+') { cnt[root.val - 'a'] += v; } dfs(root.left, v); dfs(root.right, v); } } ////// // if '-' supported, then it's just (-1*X) // 2 maps, one for + , and one for - class Solution_followup { public boolean checkEquivalence(Node root1, Node root2) { int[] countPlus = new int[26]; int[] countMinus = new int[26]; dfs(root1, countPlus, countMinus, 1, false); dfs(root2, countPlus, countMinus, -1, false); for (int i = 0; i < countPlus.length; i++) { if (countPlus[i] != 0) { return false; } } for (int i = 0; i < countMinus.length; i++) { if (countMinus[i] != 0) { return false; } } return true; } private void dfs(Node cur, int[] countPlus, int[] countMinus, int diff, boolean isRightChildOfMinusNode) { if (cur == null) { return; } if (cur.val == '+') { dfs(cur.left, countPlus, countMinus, diff, false); dfs(cur.right, countPlus, countMinus, diff, false); } else if (cur.val == '-') { dfs(cur.left, countPlus, countMinus, diff, false); dfs(cur.right, countPlus, countMinus, diff, true); } else { if (isRightChildOfMinusNode) { countMinus[cur.val - 'a'] += diff; } else { countPlus[cur.val - 'a'] += diff; } } } } -
/** * Definition for a binary tree node. * struct Node { * char val; * Node *left; * Node *right; * Node() : val(' '), left(nullptr), right(nullptr) {} * Node(char x) : val(x), left(nullptr), right(nullptr) {} * Node(char x, Node *left, Node *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: bool checkEquivalence(Node* root1, Node* root2) { int cnt[26]{}; function<void(Node*, int)> dfs = [&](Node* root, int v) { if (!root) { return; } if (root->val != '+') { cnt[root->val - 'a'] += v; } dfs(root->left, v); dfs(root->right, v); }; dfs(root1, 1); dfs(root2, -1); for (int& x : cnt) { if (x) { return false; } } return true; } }; -
# Definition for a binary tree node. # class Node(object): # def __init__(self, val=" ", left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def checkEquivalence(self, root1: 'Node', root2: 'Node') -> bool: def dfs(root, v): if root is None: return if root.val != '+': cnt[root.val] += v dfs(root.left, v) dfs(root.right, v) cnt = Counter() dfs(root1, 1) dfs(root2, -1) return all(x == 0 for x in cnt.values()) # or, return sum(cnt.values()) == 0 ############### from collections import Counter # follow-up class Solution: def checkEquivalence(self, root1: 'Node', root2: 'Node') -> bool: def traverse(node, counter): if node is None: return if node.val.isdigit(): counter[node.val] += 1 elif node.val in ('+', '-'): counter[node.val] += 1 traverse(node.left, counter) traverse(node.right, counter) counter1 = Counter() counter2 = Counter() traverse(root1, counter1) traverse(root2, counter2) return counter1 == counter2 ############# ''' >>> a = [11,22,33,44,55,11,22,33,11,22] >>> a.count(11) 3 >>> >>> a = ['aaa', 'bbb', 'ccc', 'aaa'] >>> a.count('aaa') 2 >>> a.count('zzz') 0 ''' from collections import Counter class Solution: def checkEquivalence(self, root1: 'Node', root2: 'Node') -> bool: counter = [0] * 26 def dfs(root, incr): if root: dfs(root.left, incr) dfs(root.right, incr) if root.val != '+': counter[ord(root.val) - ord('a')] += incr dfs(root1, 1) dfs(root2, -1) return counter.count(0) == 26 ############ # Definition for a binary tree node. # class Node(object): # def __init__(self, val=" ", left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def checkEquivalence(self, root1: 'Node', root2: 'Node') -> bool: def calc(ans, left, right, op): for i in range(26): if op == '+': ans[i] = left[i] + right[i] else: ans[i] = left[i] - right[i] def dfs(root): ans = [0] * 26 if not root: return ans if root.val in ['+', '-']: left, right = dfs(root.left), dfs(root.right) calc(ans, left, right, root.val) else: ans[ord(root.val) - ord('a')] += 1 return ans return dfs(root1) == dfs(root2) -
/** * Definition for a binary tree node. * function Node(val, left, right) { * this.val = (val===undefined ? " " : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } */ /** * @param {Node} root1 * @param {Node} root2 * @return {boolean} */ var checkEquivalence = function (root1, root2) { const cnt = new Array(26).fill(0); const dfs = (root, v) => { if (!root) { return; } if (root.val !== '+') { cnt[root.val.charCodeAt(0) - 'a'.charCodeAt(0)] += v; } dfs(root.left, v); dfs(root.right, v); }; dfs(root1, 1); dfs(root2, -1); for (const x of cnt) { if (x) { return false; } } return true; };