1586. Binary Search Tree Iterator II

Description

Implement the BSTIterator class that represents an iterator over the in-order traversal of a binary search tree (BST):

BSTIterator(TreeNode root) Initializes an object of the BSTIterator class. The root of the BST is given as part of the constructor. The pointer should be initialized to a non-existent number smaller than any element in the BST.
boolean hasNext() Returns true if there exists a number in the traversal to the right of the pointer, otherwise returns false.
int next() Moves the pointer to the right, then returns the number at the pointer.
boolean hasPrev() Returns true if there exists a number in the traversal to the left of the pointer, otherwise returns false.
int prev() Moves the pointer to the left, then returns the number at the pointer.

Notice that by initializing the pointer to a non-existent smallest number, the first call to next() will return the smallest element in the BST.

You may assume that next() and prev() calls will always be valid. That is, there will be at least a next/previous number in the in-order traversal when next()/prev() is called.

Example 1:

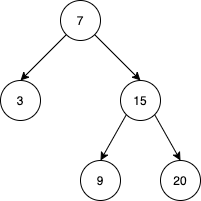
Input
["BSTIterator", "next", "next", "prev", "next", "hasNext", "next", "next", "next", "hasNext", "hasPrev", "prev", "prev"]
[[[7, 3, 15, null, null, 9, 20]], [null], [null], [null], [null], [null], [null], [null], [null], [null], [null], [null], [null]]
Output
[null, 3, 7, 3, 7, true, 9, 15, 20, false, true, 15, 9]

Explanation
// The underlined element is where the pointer currently is.
BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]); // state is   [3, 7, 9, 15, 20]
bSTIterator.next(); // state becomes [3, 7, 9, 15, 20], return 3
bSTIterator.next(); // state becomes [3, 7, 9, 15, 20], return 7
bSTIterator.prev(); // state becomes [3, 7, 9, 15, 20], return 3
bSTIterator.next(); // state becomes [3, 7, 9, 15, 20], return 7
bSTIterator.hasNext(); // return true
bSTIterator.next(); // state becomes [3, 7, 9, 15, 20], return 9
bSTIterator.next(); // state becomes [3, 7, 9, 15, 20], return 15
bSTIterator.next(); // state becomes [3, 7, 9, 15, 20], return 20
bSTIterator.hasNext(); // return false
bSTIterator.hasPrev(); // return true
bSTIterator.prev(); // state becomes [3, 7, 9, 15, 20], return 15
bSTIterator.prev(); // state becomes [3, 7, 9, 15, 20], return 9

Constraints:

The number of nodes in the tree is in the range [1, 10⁵].
0 <= Node.val <= 10⁶
At most 10⁵ calls will be made to hasNext, next, hasPrev, and prev.

Follow up: Could you solve the problem without precalculating the values of the tree?

Solutions

Solution 1: In-order Traversal + Array

We can use in-order traversal to store the values of all nodes in the binary search tree into an array $nums$, and then use the array to implement the iterator. We define a pointer $i$, initially $i = -1$, which points to an element in the array $nums$. Each time we call $next()$, we add $1$ to the value of $i$ and return $nums[i]$; each time we call $prev()$, we subtract $1$ from the value of $i$ and return $nums[i]$.

In terms of time complexity, initializing the iterator requires $O(n)$ time, where $n$ is the number of nodes in the binary search tree. Each call to $next()$ and $prev()$ requires $O(1)$ time. In terms of space complexity, we need $O(n)$ space to store the values of all nodes in the binary search tree.

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class BSTIterator {
    private List<Integer> nums = new ArrayList<>();
    private int i = -1;

    public BSTIterator(TreeNode root) {
        dfs(root);
    }

    public boolean hasNext() {
        return i < nums.size() - 1;
    }

    public int next() {
        return nums.get(++i);
    }

    public boolean hasPrev() {
        return i > 0;
    }

    public int prev() {
        return nums.get(--i);
    }

    private void dfs(TreeNode root) {
        if (root == null) {
            return;
        }
        dfs(root.left);
        nums.add(root.val);
        dfs(root.right);
    }
}

/**
 * Your BSTIterator object will be instantiated and called as such:
 * BSTIterator obj = new BSTIterator(root);
 * boolean param_1 = obj.hasNext();
 * int param_2 = obj.next();
 * boolean param_3 = obj.hasPrev();
 * int param_4 = obj.prev();
 */

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class BSTIterator {
public:
    BSTIterator(TreeNode* root) {
        dfs(root);
        n = nums.size();
    }

    bool hasNext() {
        return i < n - 1;
    }

    int next() {
        return nums[++i];
    }

    bool hasPrev() {
        return i > 0;
    }

    int prev() {
        return nums[--i];
    }

private:
    vector<int> nums;
    int i = -1;
    int n;

    void dfs(TreeNode* root) {
        if (!root) {
            return;
        }
        dfs(root->left);
        nums.push_back(root->val);
        dfs(root->right);
    }
};

/**
 * Your BSTIterator object will be instantiated and called as such:
 * BSTIterator* obj = new BSTIterator(root);
 * bool param_1 = obj->hasNext();
 * int param_2 = obj->next();
 * bool param_3 = obj->hasPrev();
 * int param_4 = obj->prev();
 */

class BSTIterator: # lazy load, not create full doubly-linked list

    def __init__(self, root: Optional[TreeNode]):

        self.next_stack = [] # 记录所有还没有被 visited 的node
        self.prev_stack = [] # 记录所有被 visited 的node
        self.ind = 0 #当前node的位置
        # 从根节点开始把所有左边节点放进stack
        # 从大到小放到nextstack， nextstack的最后一个是当前最小节点
        while root:
            self.next_stack.append(root)
            root = root.left

    def hasNext(self) -> bool:
        # 还有节点没有被visited OR 所有节点都被visited 但是当前节点不是最后一个节点
        return len(self.next_stack) > 0 or self.ind + 1 < len(self.prev_stack)


    def next(self) -> int:

        # 当前节点是已经在stack里 且不是最后一个
        if self.ind + 1 < len(self.prev_stack):
            self.ind += 1
            return self.prev_stack[self.ind].val

        # 当前节点是stack里的最后一个， 继续看nextstack里是否有下一个节点
        node = self.next_stack.pop()

        # 把nextstack里的节点pop出来加到stack里
        # 把index reset指向stack里的最后一个节点 -- 当前节点
        self.prev_stack.append(node)
        self.ind = len(self.prev_stack) - 1

        # 如果当前node有右子树，把右子树的左节点加到next里，从大到小的顺序从而使 nextstack里的最新一个node是当前最小的
        current = node.right
        while current:
            self.next_stack.append(current)
            current = current.left

        return node.val

    def hasPrev(self) -> bool:
        # 如果index >= 1 则说明stack里有前一个节点 stack[0]
        return self.ind != 0

    def prev(self) -> int:
        # 把当前index往前移1 然后return
        # later that index will be overwritten
        self.ind -= 1
        return self.prev_stack[self.ind].val

#############

class BSTIterator: # extra space, to save the list
    def __init__(self, root):
        self.dummyHead = TreeNode(0)
        self.curr = None

        stack = []
        prev = self.dummyHead
        node = root

        # in-order traversal, iteratively
        while node or stack:
            if node:
                stack.append(node)
                node = node.left
            else:
                node = stack.pop()
                # re-contruct a double-linked-list, re-use TreeNode class as actual LinkNode
                visitNode = TreeNode(node.val)
                prev.right = visitNode
                visitNode.left = prev
                prev = visitNode
                node = node.right

        self.curr = self.dummyHead

    def hasNext(self):
        return self.curr.right is not None

    def next(self):
        self.curr = self.curr.right
        return self.curr.val

    def hasPrev(self):
        return self.curr.left != self.dummyHead and self.curr != self.dummyHead

    def prev(self):
        self.curr = self.curr.left
        return self.curr.val

###############

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class BSTIterator:
    def __init__(self, root: Optional[TreeNode]):
        self.nums = []

        def dfs(root):
            if root is None:
                return
            dfs(root.left)
            self.nums.append(root.val)
            dfs(root.right)

        dfs(root)
        self.i = -1

    def hasNext(self) -> bool:
        return self.i < len(self.nums) - 1

    def next(self) -> int:
        self.i += 1
        return self.nums[self.i]

    def hasPrev(self) -> bool:
        return self.i > 0

    def prev(self) -> int:
        self.i -= 1
        return self.nums[self.i]


# Your BSTIterator object will be instantiated and called as such:
# obj = BSTIterator(root)
# param_1 = obj.hasNext()
# param_2 = obj.next()
# param_3 = obj.hasPrev()
# param_4 = obj.prev()

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
type BSTIterator struct {
	nums []int
	i, n int
}

func Constructor(root *TreeNode) BSTIterator {
	nums := []int{}
	var dfs func(*TreeNode)
	dfs = func(root *TreeNode) {
		if root == nil {
			return
		}
		dfs(root.Left)
		nums = append(nums, root.Val)
		dfs(root.Right)
	}
	dfs(root)
	return BSTIterator{nums, -1, len(nums)}
}

func (this *BSTIterator) HasNext() bool {
	return this.i < this.n-1
}

func (this *BSTIterator) Next() int {
	this.i++
	return this.nums[this.i]
}

func (this *BSTIterator) HasPrev() bool {
	return this.i > 0
}

func (this *BSTIterator) Prev() int {
	this.i--
	return this.nums[this.i]
}

/**
 * Your BSTIterator object will be instantiated and called as such:
 * obj := Constructor(root);
 * param_1 := obj.HasNext();
 * param_2 := obj.Next();
 * param_3 := obj.HasPrev();
 * param_4 := obj.Prev();
 */

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

class BSTIterator {
    private nums: number[];
    private n: number;
    private i: number;

    constructor(root: TreeNode | null) {
        this.nums = [];
        const dfs = (root: TreeNode | null) => {
            if (!root) {
                return;
            }
            dfs(root.left);
            this.nums.push(root.val);
            dfs(root.right);
        };
        dfs(root);
        this.n = this.nums.length;
        this.i = -1;
    }

    hasNext(): boolean {
        return this.i < this.n - 1;
    }

    next(): number {
        return this.nums[++this.i];
    }

    hasPrev(): boolean {
        return this.i > 0;
    }

    prev(): number {
        return this.nums[--this.i];
    }
}

/**
 * Your BSTIterator object will be instantiated and called as such:
 * var obj = new BSTIterator(root)
 * var param_1 = obj.hasNext()
 * var param_2 = obj.next()
 * var param_3 = obj.hasPrev()
 * var param_4 = obj.prev()
 */

1586 - Binary Search Tree Iterator II

1586. Binary Search Tree Iterator II

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

1586. Binary Search Tree Iterator II

Description

Solutions

All Problems

All Solutions