1568. Minimum Number of Days to Disconnect Island

Description

You are given an m x n binary grid grid where 1 represents land and 0 represents water. An island is a maximal 4-directionally (horizontal or vertical) connected group of 1's.

The grid is said to be connected if we have exactly one island, otherwise is said disconnected.

In one day, we are allowed to change any single land cell (1) into a water cell (0).

Return the minimum number of days to disconnect the grid.

Example 1:

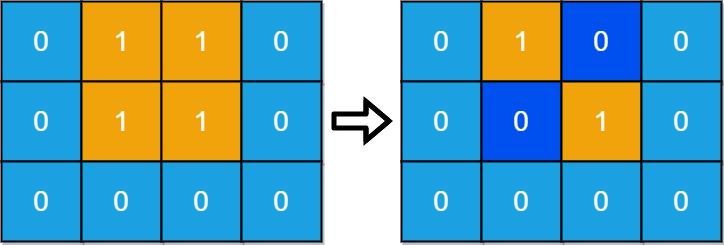
Input: grid = [[0,1,1,0],[0,1,1,0],[0,0,0,0]]

Output: 2
Explanation: We need at least 2 days to get a disconnected grid.
Change land grid[1][1] and grid[0][2] to water and get 2 disconnected island.

Example 2:

Input: grid = [[1,1]]
Output: 2
Explanation: Grid of full water is also disconnected ([[1,1]] -> [[0,0]]), 0 islands.

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 30
grid[i][j] is either 0 or 1.

Solutions

class Solution {
    private static final int[] DIRS = new int[] {-1, 0, 1, 0, -1};
    private int[][] grid;
    private int m;
    private int n;

    public int minDays(int[][] grid) {
        this.grid = grid;
        m = grid.length;
        n = grid[0].length;
        if (count() != 1) {
            return 0;
        }
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 1) {
                    grid[i][j] = 0;
                    if (count() != 1) {
                        return 1;
                    }
                    grid[i][j] = 1;
                }
            }
        }
        return 2;
    }

    private int count() {
        int cnt = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 1) {
                    dfs(i, j);
                    ++cnt;
                }
            }
        }
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 2) {
                    grid[i][j] = 1;
                }
            }
        }
        return cnt;
    }

    private void dfs(int i, int j) {
        grid[i][j] = 2;
        for (int k = 0; k < 4; ++k) {
            int x = i + DIRS[k], y = j + DIRS[k + 1];
            if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1) {
                dfs(x, y);
            }
        }
    }
}

class Solution {
public:
    const vector<int> dirs = {-1, 0, 1, 0, -1};
    int m, n;

    int minDays(vector<vector<int>>& grid) {
        m = grid.size(), n = grid[0].size();
        if (count(grid) != 1) {
            return 0;
        }
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 1) {
                    grid[i][j] = 0;
                    if (count(grid) != 1) {
                        return 1;
                    }
                    grid[i][j] = 1;
                }
            }
        }
        return 2;
    }

    int count(vector<vector<int>>& grid) {
        int cnt = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 1) {
                    dfs(i, j, grid);
                    ++cnt;
                }
            }
        }
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 2) {
                    grid[i][j] = 1;
                }
            }
        }
        return cnt;
    }

    void dfs(int i, int j, vector<vector<int>>& grid) {
        grid[i][j] = 2;
        for (int k = 0; k < 4; ++k) {
            int x = i + dirs[k], y = j + dirs[k + 1];
            if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1) {
                dfs(x, y, grid);
            }
        }
    }
};

class Solution:
    def minDays(self, grid: List[List[int]]) -> int:
        if self.count(grid) != 1:
            return 0
        m, n = len(grid), len(grid[0])
        for i in range(m):
            for j in range(n):
                if grid[i][j] == 1:
                    grid[i][j] = 0
                    if self.count(grid) != 1:
                        return 1
                    grid[i][j] = 1
        return 2

    def count(self, grid):
        def dfs(i, j):
            grid[i][j] = 2
            for a, b in [[0, -1], [0, 1], [1, 0], [-1, 0]]:
                x, y = i + a, j + b
                if 0 <= x < m and 0 <= y < n and grid[x][y] == 1:
                    dfs(x, y)

        m, n = len(grid), len(grid[0])
        cnt = 0
        for i in range(m):
            for j in range(n):
                if grid[i][j] == 1:
                    dfs(i, j)
                    cnt += 1
        for i in range(m):
            for j in range(n):
                if grid[i][j] == 2:
                    grid[i][j] = 1
        return cnt

func minDays(grid [][]int) int {
	m, n := len(grid), len(grid[0])
	dirs := []int{-1, 0, 1, 0, -1}

	var dfs func(i, j int)
	dfs = func(i, j int) {
		grid[i][j] = 2
		for k := 0; k < 4; k++ {
			x, y := i+dirs[k], j+dirs[k+1]
			if x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1 {
				dfs(x, y)
			}
		}
	}

	count := func() int {
		cnt := 0
		for i := 0; i < m; i++ {
			for j := 0; j < n; j++ {
				if grid[i][j] == 1 {
					dfs(i, j)
					cnt++
				}
			}
		}
		for i := 0; i < m; i++ {
			for j := 0; j < n; j++ {
				if grid[i][j] == 2 {
					grid[i][j] = 1
				}
			}
		}
		return cnt
	}

	if count() != 1 {
		return 0
	}
	for i := 0; i < m; i++ {
		for j := 0; j < n; j++ {
			if grid[i][j] == 1 {
				grid[i][j] = 0
				if count() != 1 {
					return 1
				}
				grid[i][j] = 1
			}
		}
	}
	return 2
}

/**
 * @param {number[][]} grid
 * @return {number}
 */
var minDays = function (grid) {
    const directions = [
        [0, 1],
        [1, 0],
        [0, -1],
        [-1, 0],
    ];
    const rows = grid.length;
    const cols = grid[0].length;

    function dfs(x, y, visited) {
        visited[x][y] = true;
        for (let [dx, dy] of directions) {
            const nx = x + dx,
                ny = y + dy;
            if (
                nx >= 0 &&
                ny >= 0 &&
                nx < rows &&
                ny < cols &&
                grid[nx][ny] === 1 &&
                !visited[nx][ny]
            ) {
                dfs(nx, ny, visited);
            }
        }
    }

    function countIslands() {
        let visited = Array.from({ length: rows }, () => Array(cols).fill(false));
        let count = 0;
        for (let i = 0; i < rows; i++) {
            for (let j = 0; j < cols; j++) {
                if (grid[i][j] === 1 && !visited[i][j]) {
                    count++;
                    dfs(i, j, visited);
                }
            }
        }
        return count;
    }

    if (countIslands() !== 1) return 0;

    for (let i = 0; i < rows; i++) {
        for (let j = 0; j < cols; j++) {
            if (grid[i][j] === 1) {
                grid[i][j] = 0;
                if (countIslands() !== 1) return 1;
                grid[i][j] = 1;
            }
        }
    }

    return 2;
};

function minDays(grid: number[][]): number {
    const [m, n] = [grid.length, grid[0].length];

    const dfs = (i: number, j: number) => {
        if (i < 0 || m <= i || j < 0 || n <= j || [0, 2].includes(grid[i][j])) return;

        grid[i][j] = 2;
        const dir = [-1, 0, 1, 0, -1];
        for (let k = 0; k < 4; k++) {
            const [y, x] = [i + dir[k], j + dir[k + 1]];
            dfs(y, x);
        }
    };

    const count = () => {
        let c = 0;

        for (let i = 0; i < m; i++) {
            for (let j = 0; j < n; j++) {
                if (grid[i][j] === 1) {
                    dfs(i, j);
                    c++;
                }
            }
        }

        for (let i = 0; i < m; i++) {
            for (let j = 0; j < n; j++) {
                if (grid[i][j] === 2) {
                    grid[i][j] = 1;
                }
            }
        }

        return c;
    };

    if (count() !== 1) return 0;

    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            if (grid[i][j] === 1) {
                grid[i][j] = 0;

                if (count() !== 1) return 1;

                grid[i][j] = 1;
            }
        }
    }

    return 2;
}

1568 - Minimum Number of Days to Disconnect Island

1568. Minimum Number of Days to Disconnect Island

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

1568. Minimum Number of Days to Disconnect Island

Description

Solutions

All Problems

All Solutions