Welcome to Subscribe On Youtube

Formatted question description: https://leetcode.ca/all/1516.html

1516. Move Sub-Tree of N-Ary Tree

Level

Hard

Description

Given the root of an N-ary tree of unique values, and two nodes of the tree p and q.

You should move the subtree of the node p to become a direct child of node q. If p is already a direct child of q, don’t change anything. Node p must be the last child in the children list of node q.

Return the root of the tree after adjusting it.

There are 3 cases for nodes p and q:

  1. Node q is in the sub-tree of node p.
  2. Node p is in the sub-tree of node q.
  3. Neither node p is in the sub-tree of node q nor node q is in the sub-tree of node p.

In cases 2 and 3, you just need to move p (with its sub-tree) to be a child of q, but in case 1 the tree may be disconnected, thus you need to reconnect the tree again. Please read the examples carefully before solving this problem.

Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples).

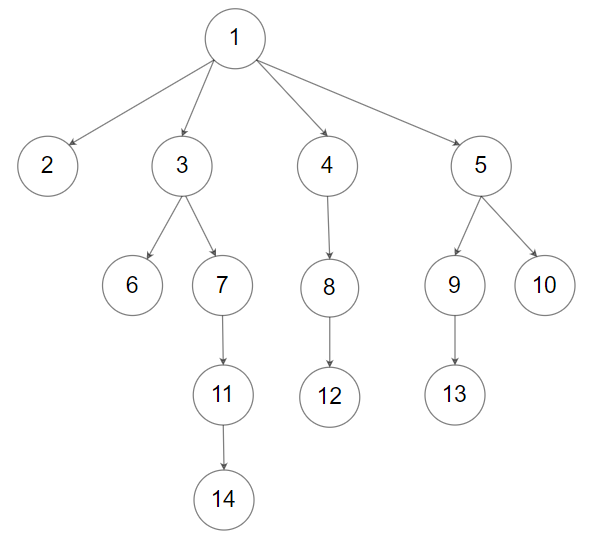
Image text

For example, the above tree is serialized as [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14].

Example 1:

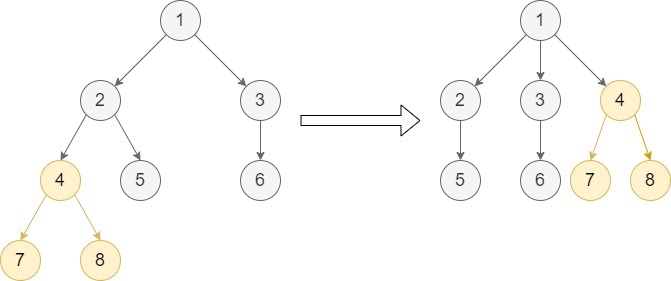
Image text

Input: root = [1,null,2,3,null,4,5,null,6,null,7,8], p = 4, q = 1

Output: [1,null,2,3,4,null,5,null,6,null,7,8]

Explanation: This example follows the second case as node p is in the sub-tree of node q. We move node p with its sub-tree to be a direct child of node q.

Notice that node 4 is the last child of node 1.

Example 2:

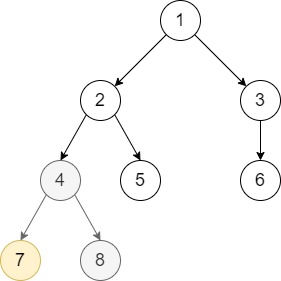
Image text

Input: root = [1,null,2,3,null,4,5,null,6,null,7,8], p = 7, q = 4

Output: [1,null,2,3,null,4,5,null,6,null,7,8]

Explanation: Node 7 is already a direct child of node 4. We don’t change anything.

Example 3:

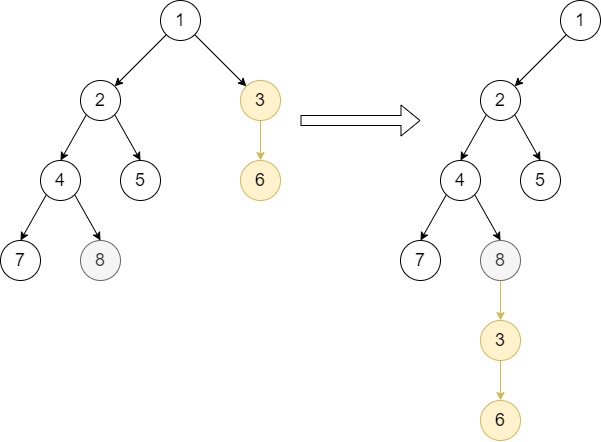
Image text

Input: root = [1,null,2,3,null,4,5,null,6,null,7,8], p = 3, q = 8

Output: [1,null,2,null,4,5,null,7,8,null,null,null,3,null,6]

Explanation: This example follows case 3 because node p is not in the sub-tree of node q and vice-versa. We can move node 3 with its sub-tree and make it as node 8’s child.

Example 4:

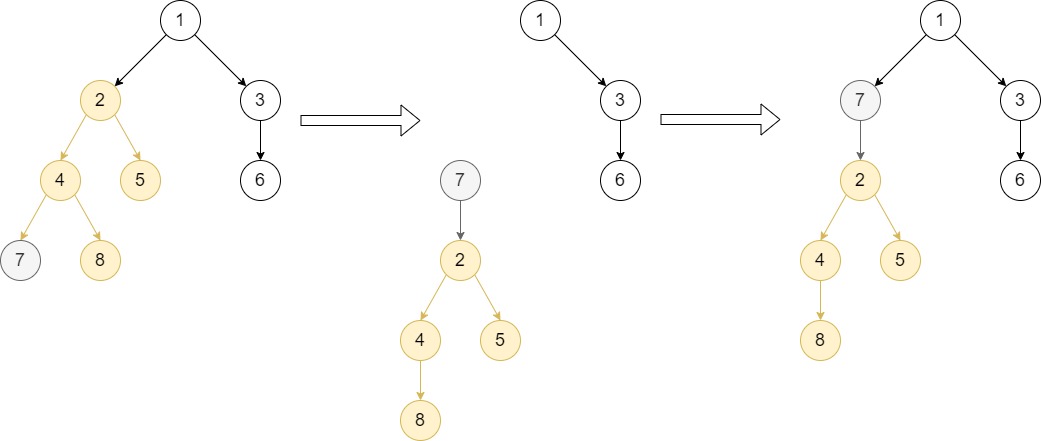
Image text

Input: root = [1,null,2,3,null,4,5,null,6,null,7,8], p = 2, q = 7

Output: [1,null,7,3,null,2,null,6,null,4,5,null,null,8]

Explanation: Node q is in the sub-tree of node p, so this is case 1.

The first step, we move node p (with all of its sub-tree except for node q) and add it as a child to node q.

Then we will see that the tree is disconnected, you need to reconnect node q to replace node p as shown.

Example 5:

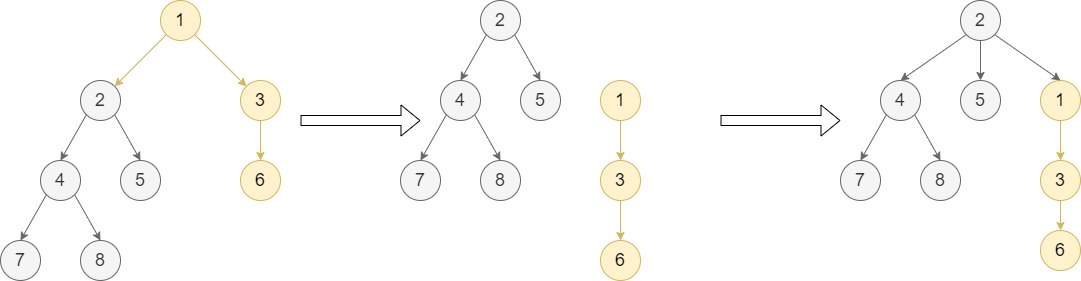
Image text

Input: root = [1,null,2,3,null,4,5,null,6,null,7,8], p = 1, q = 2

Output: [2,null,4,5,1,null,7,8,null,null,3,null,null,null,6]

Explanation: Node q is in the sub-tree of node p, so this is case 1. The first step, we move node p (with all of its sub-tree except for node q) and add it as a child to node q.

As node p was the root of the tree, node q replaces it and becomes the root of the tree.

Constraints:

  • The total number of nodes is between [2, 1000].
  • Each node has a unique value.
  • p != null
  • q != null
  • p and q are two different nodes (i.e. p != q).

Solution

Do depth first search to find each node’s parent. If node q is already the parent of node p, then simply return the original tree.

Otherwise, check whether node q is in the subtree of node p. If node p is not the root of the N-ary tree, then if node q is in the subtree of node p, remove node q from its parent’s children and replace node p with node q in node p’s children. If node q is not in the subtree of node p, remove node p from its parent’s children. Finally add node p to node q’s children, and return the N-ary tree’s root.

If node p is the root of the N-ary tree, then remove node q from its parent’s children, add node p to node q’s children, and return node q as the root of the new N-ary tree.

  • /*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> children;

    
    public Node() {
        children = new ArrayList<Node>();
    }
    
    public Node(int _val) {
        val = _val;
        children = new ArrayList<Node>();
    }
    
    public Node(int _val,ArrayList<Node> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
    public Node moveSubTree(Node root, Node p, Node q) {
        Map<Node, Node> parentMap = new HashMap<Node, Node>();
        Deque<Node> stack = new LinkedList<Node>();
        stack.push(root);
        while (!stack.isEmpty()) {
            Node node = stack.pop();
            List<Node> children = node.children;
            for (int i = children.size() - 1; i >= 0; i--) {
                Node child = children.get(i);
                parentMap.put(child, node);
                stack.push(child);
            }
        }
        if (parentMap.get(p) == q)
            return root;
        boolean flag = false;
        Node temp = q;
        while (temp != null) {
            Node parent = parentMap.get(temp);
            if (parent == p) {
                flag = true;
                break;
            } else
                temp = parent;
        }
        if (parentMap.containsKey(p)) {
            Node pParent = parentMap.get(p);
            if (flag) {
                Node qParent = parentMap.get(q);
                qParent.children.remove(q);
                int index = pParent.children.indexOf(p);
                pParent.children.set(index, q);
            } else
                pParent.children.remove(p);
            q.children.add(p);
            return root;
        } else {
            Node qParent = parentMap.get(q);
            qParent.children.remove(q);
            q.children.add(p);
            return q;
        }
    }
}

All Problems

All Solutions