Welcome to Subscribe On Youtube
1514. Path with Maximum Probability
Description
You are given an undirected weighted graph of n nodes (0-indexed), represented by an edge list where edges[i] = [a, b] is an undirected edge connecting the nodes a and b with a probability of success of traversing that edge succProb[i].
Given two nodes start and end, find the path with the maximum probability of success to go from start to end and return its success probability.
If there is no path from start to end, return 0. Your answer will be accepted if it differs from the correct answer by at most 1e-5.
Example 1:
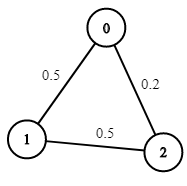
Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2 Output: 0.25000 Explanation: There are two paths from start to end, one having a probability of success = 0.2 and the other has 0.5 * 0.5 = 0.25.
Example 2:
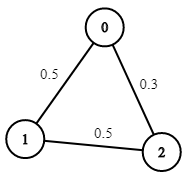
Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2 Output: 0.30000
Example 3:
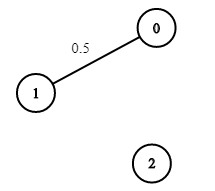
Input: n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2 Output: 0.00000 Explanation: There is no path between 0 and 2.
Constraints:
2 <= n <= 10^40 <= start, end < nstart != end0 <= a, b < na != b0 <= succProb.length == edges.length <= 2*10^40 <= succProb[i] <= 1- There is at most one edge between every two nodes.
Solutions
-
class Solution { public double maxProbability(int n, int[][] edges, double[] succProb, int start, int end) { List<Pair<Integer, Double>>[] g = new List[n]; Arrays.setAll(g, k -> new ArrayList<>()); for (int i = 0; i < edges.length; ++i) { int a = edges[i][0], b = edges[i][1]; double s = succProb[i]; g[a].add(new Pair<>(b, s)); g[b].add(new Pair<>(a, s)); } PriorityQueue<Pair<Double, Integer>> q = new PriorityQueue<>(Comparator.comparingDouble(Pair::getKey)); double[] d = new double[n]; d[start] = 1.0; q.offer(new Pair<>(-1.0, start)); while (!q.isEmpty()) { Pair<Double, Integer> p = q.poll(); double w = p.getKey(); w *= -1; int u = p.getValue(); for (Pair<Integer, Double> ne : g[u]) { int v = ne.getKey(); double t = ne.getValue(); if (d[v] < d[u] * t) { d[v] = d[u] * t; q.offer(new Pair<>(-d[v], v)); } } } return d[end]; } } -
class Solution { public: double maxProbability(int n, vector<vector<int>>& edges, vector<double>& succProb, int start, int end) { vector<vector<pair<int, double>>> g(n); for (int i = 0; i < edges.size(); ++i) { int a = edges[i][0], b = edges[i][1]; double s = succProb[i]; g[a].push_back({b, s}); g[b].push_back({a, s}); } vector<double> d(n); d[start] = 1.0; queue<pair<double, int>> q; q.push({1.0, start}); while (!q.empty()) { auto p = q.front(); q.pop(); double w = p.first; int u = p.second; if (d[u] > w) continue; for (auto& e : g[u]) { int v = e.first; double t = e.second; if (d[v] < d[u] * t) { d[v] = d[u] * t; q.push({d[v], v}); } } } return d[end]; } }; -
class Solution: def maxProbability( self, n: int, edges: List[List[int]], succProb: List[float], start: int, end: int, ) -> float: g = defaultdict(list) for (a, b), s in zip(edges, succProb): g[a].append((b, s)) g[b].append((a, s)) q = [(-1, start)] d = [0] * n d[start] = 1 while q: w, u = heappop(q) w = -w if d[u] > w: continue for v, t in g[u]: if d[v] < d[u] * t: d[v] = d[u] * t heappush(q, (-d[v], v)) return d[end] -
func maxProbability(n int, edges [][]int, succProb []float64, start int, end int) float64 { g := make([][]pair, n) for i, e := range edges { a, b, s := e[0], e[1], succProb[i] g[a] = append(g[a], pair{b, s}) g[b] = append(g[b], pair{a, s}) } d := make([]float64, n) d[start] = 1 vis := make([]bool, n) q := []int{start} vis[start] = true for len(q) > 0 { i := q[0] q = q[1:] vis[i] = false for _, ne := range g[i] { j, s := ne.idx, ne.s if d[j] < d[i]*s { d[j] = d[i] * s if !vis[j] { q = append(q, j) vis[j] = true } } } } return d[end] } type pair struct { idx int s float64 }