Welcome to Subscribe On Youtube

1504. Count Submatrices With All Ones

Description

Given an m x n binary matrix mat, return the number of submatrices that have all ones.

 

Example 1:

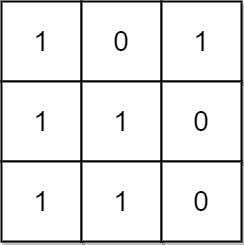
Input: mat = [[1,0,1],[1,1,0],[1,1,0]]
Output: 13
Explanation: 
There are 6 rectangles of side 1x1.
There are 2 rectangles of side 1x2.
There are 3 rectangles of side 2x1.
There is 1 rectangle of side 2x2. 
There is 1 rectangle of side 3x1.
Total number of rectangles = 6 + 2 + 3 + 1 + 1 = 13.

Example 2:

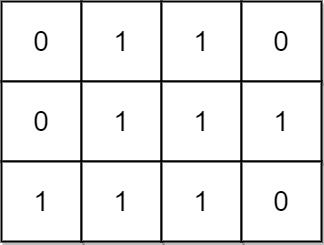
Input: mat = [[0,1,1,0],[0,1,1,1],[1,1,1,0]]
Output: 24
Explanation: 
There are 8 rectangles of side 1x1.
There are 5 rectangles of side 1x2.
There are 2 rectangles of side 1x3. 
There are 4 rectangles of side 2x1.
There are 2 rectangles of side 2x2. 
There are 2 rectangles of side 3x1. 
There is 1 rectangle of side 3x2. 
Total number of rectangles = 8 + 5 + 2 + 4 + 2 + 2 + 1 = 24.

 

Constraints:

• 1 <= m, n <= 150
• mat[i][j] is either 0 or 1.

Solutions

• Java
• C++
• Python
• Go

• class Solution {
      public int numSubmat(int[][] mat) {
          int m = mat.length, n = mat[0].length;
          int[][] g = new int[m][n];
          for (int i = 0; i < m; ++i) {
              for (int j = 0; j < n; ++j) {
                  if (mat[i][j] == 1) {
                      g[i][j] = j == 0 ? 1 : 1 + g[i][j - 1];
                  }
              }
          }
          int ans = 0;
          for (int i = 0; i < m; ++i) {
              for (int j = 0; j < n; ++j) {
                  int col = 1 << 30;
                  for (int k = i; k >= 0 && col > 0; --k) {
                      col = Math.min(col, g[k][j]);
                      ans += col;
                  }
              }
          }
          return ans;
      }
  }
  

• class Solution {
  public:
      int numSubmat(vector<vector<int>>& mat) {
          int m = mat.size(), n = mat[0].size();
          vector<vector<int>> g(m, vector<int>(n));
          for (int i = 0; i < m; ++i) {
              for (int j = 0; j < n; ++j) {
                  if (mat[i][j] == 1) {
                      g[i][j] = j == 0 ? 1 : 1 + g[i][j - 1];
                  }
              }
          }
          int ans = 0;
          for (int i = 0; i < m; ++i) {
              for (int j = 0; j < n; ++j) {
                  int col = 1 << 30;
                  for (int k = i; k >= 0 && col > 0; --k) {
                      col = min(col, g[k][j]);
                      ans += col;
                  }
              }
          }
          return ans;
      }
  };
  

• class Solution:
      def numSubmat(self, mat: List[List[int]]) -> int:
          m, n = len(mat), len(mat[0])
          g = [[0] * n for _ in range(m)]
          for i in range(m):
              for j in range(n):
                  if mat[i][j]:
                      g[i][j] = 1 if j == 0 else 1 + g[i][j - 1]
          ans = 0
          for i in range(m):
              for j in range(n):
                  col = inf
                  for k in range(i, -1, -1):
                      col = min(col, g[k][j])
                      ans += col
          return ans
  
  

• func numSubmat(mat [][]int) (ans int) {
  	m, n := len(mat), len(mat[0])
  	g := make([][]int, m)
  	for i := range g {
  		g[i] = make([]int, n)
  		for j := range g[i] {
  			if mat[i][j] == 1 {
  				if j == 0 {
  					g[i][j] = 1
  				} else {
  					g[i][j] = 1 + g[i][j-1]
  				}
  			}
  		}
  	}
  	for i := range g {
  		for j := range g[i] {
  			col := 1 << 30
  			for k := i; k >= 0 && col > 0; k-- {
  				col = min(col, g[k][j])
  				ans += col
  			}
  		}
  	}
  	return
  }
  

All Problems

All Solutions