1504. Count Submatrices With All Ones

Description

Given an m x n binary matrix mat, return the number of submatrices that have all ones.

Example 1:

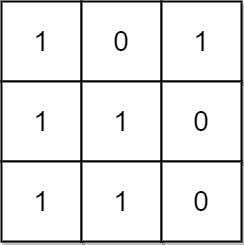
Input: mat = [[1,0,1],[1,1,0],[1,1,0]]
Output: 13
Explanation: 
There are 6 rectangles of side 1x1.
There are 2 rectangles of side 1x2.
There are 3 rectangles of side 2x1.
There is 1 rectangle of side 2x2. 
There is 1 rectangle of side 3x1.
Total number of rectangles = 6 + 2 + 3 + 1 + 1 = 13.

Example 2:

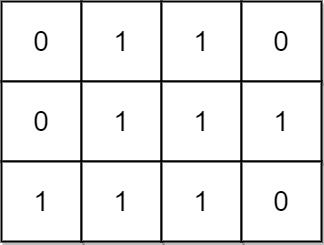
Input: mat = [[0,1,1,0],[0,1,1,1],[1,1,1,0]]
Output: 24
Explanation: 
There are 8 rectangles of side 1x1.
There are 5 rectangles of side 1x2.
There are 2 rectangles of side 1x3. 
There are 4 rectangles of side 2x1.
There are 2 rectangles of side 2x2. 
There are 2 rectangles of side 3x1. 
There is 1 rectangle of side 3x2. 
Total number of rectangles = 8 + 5 + 2 + 4 + 2 + 2 + 1 = 24.

Constraints:

1 <= m, n <= 150
mat[i][j] is either 0 or 1.

Solutions

Solution 2: Monotonic Stack

Thinking

Solution 1 still walks $O(m)$ rows upward at every bottom-right cell and adds the running minimum width, so the total stays $O(m^2 \times n)$. With side length $150$, that inner scan is the remaining cost.

A narrower width on the same column caps every row above it, so those rows do not need another pass. One strictly increasing stack of widths per column makes the stack top the nearest smaller width above the current cell. Between that top and the current row the minimum width is $g[i][j]$, and the answer at the top and above is already stored. Each cell is pushed and popped at most once, which turns the upward scan into amortized $O(1)$.

We still preprocess a 2D array $g$, where $g[i][j]$ is the number of consecutive $1$s from column $j$ to the left in row $i$.

The count is then taken column by column. For column $j$, scan row $i$ from top to bottom and keep a monotonic stack of triples $(w, r, c)$: the width $w$, the row $r$, and the number $c$ of all-$1$ submatrices whose bottom-right corner is $(r, j)$. Widths on the stack stay strictly increasing.

When handling $g[i][j]$, pop every stack top whose width is at least the current value. If the stack is empty, every row from $0$ through $i$ has minimum width $g[i][j]$, so there are $g[i][j] \times (i + 1)$ submatrices with bottom-right corner $(i, j)$. Otherwise let the top be $(w, r, c)$. The contribution of row $r$ and above is already stored in $c$, and every row from $r + 1$ through $i$ has minimum width $g[i][j]$, so the count is $c + g[i][j] \times (i - r)$. Add this value to the answer, then push the current width, the row index, and the count onto the stack.

The time complexity is $O(m \times n)$, and the space complexity is $O(m \times n)$. Here, $m$ and $n$ are the number of rows and columns of the matrix, respectively.

class Solution {
    public int numSubmat(int[][] mat) {
        int m = mat.length, n = mat[0].length;
        int[][] g = new int[m][n];
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (mat[i][j] == 1) {
                    g[i][j] = j == 0 ? 1 : 1 + g[i][j - 1];
                }
            }
        }
        int ans = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                int col = 1 << 30;
                for (int k = i; k >= 0 && col > 0; --k) {
                    col = Math.min(col, g[k][j]);
                    ans += col;
                }
            }
        }
        return ans;
    }
}


// Solution 2
class Solution {
    public int numSubmat(int[][] mat) {
        int m = mat.length, n = mat[0].length;
        int[][] g = new int[m][n];
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (mat[i][j] == 1) {
                    g[i][j] = j == 0 ? 1 : 1 + g[i][j - 1];
                }
            }
        }
        int ans = 0;
        for (int j = 0; j < n; ++j) {
            List<int[]> stk = new ArrayList<>();
            for (int i = 0; i < m; ++i) {
                int cur = g[i][j];
                while (!stk.isEmpty() && stk.get(stk.size() - 1)[0] >= cur) {
                    stk.remove(stk.size() - 1);
                }
                int cnt = cur * (i + 1);
                if (!stk.isEmpty()) {
                    int[] t = stk.get(stk.size() - 1);
                    cnt = t[2] + cur * (i - t[1]);
                }
                ans += cnt;
                stk.add(new int[] {cur, i, cnt});
            }
        }
        return ans;
    }
}

class Solution {
public:
    int numSubmat(vector<vector<int>>& mat) {
        int m = mat.size(), n = mat[0].size();
        vector<vector<int>> g(m, vector<int>(n));
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (mat[i][j] == 1) {
                    g[i][j] = j == 0 ? 1 : 1 + g[i][j - 1];
                }
            }
        }
        int ans = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                int col = 1 << 30;
                for (int k = i; k >= 0 && col > 0; --k) {
                    col = min(col, g[k][j]);
                    ans += col;
                }
            }
        }
        return ans;
    }
};


// Solution 2
class Solution {
public:
    int numSubmat(vector<vector<int>>& mat) {
        int m = mat.size(), n = mat[0].size();
        vector<vector<int>> g(m, vector<int>(n));
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (mat[i][j] == 1) {
                    g[i][j] = j == 0 ? 1 : 1 + g[i][j - 1];
                }
            }
        }
        int ans = 0;
        for (int j = 0; j < n; ++j) {
            vector<array<int, 3>> stk;
            for (int i = 0; i < m; ++i) {
                int cur = g[i][j];
                while (!stk.empty() && stk.back()[0] >= cur) {
                    stk.pop_back();
                }
                int cnt = cur * (i + 1);
                if (!stk.empty()) {
                    cnt = stk.back()[2] + cur * (i - stk.back()[1]);
                }
                ans += cnt;
                stk.push_back({cur, i, cnt});
            }
        }
        return ans;
    }
};

class Solution:
    def numSubmat(self, mat: List[List[int]]) -> int:
        m, n = len(mat), len(mat[0])
        g = [[0] * n for _ in range(m)]
        for i in range(m):
            for j in range(n):
                if mat[i][j]:
                    g[i][j] = 1 if j == 0 else 1 + g[i][j - 1]
        ans = 0
        for i in range(m):
            for j in range(n):
                col = inf
                for k in range(i, -1, -1):
                    col = min(col, g[k][j])
                    ans += col
        return ans



# Solution 2
class Solution:
    def numSubmat(self, mat: List[List[int]]) -> int:
        m, n = len(mat), len(mat[0])
        g = [[0] * n for _ in range(m)]
        for i in range(m):
            for j in range(n):
                if mat[i][j]:
                    g[i][j] = 1 if j == 0 else 1 + g[i][j - 1]
        ans = 0
        for j in range(n):
            stk = []
            for i in range(m):
                cur = g[i][j]
                while stk and stk[-1][0] >= cur:
                    stk.pop()
                cnt = cur * (i + 1)
                if stk:
                    cnt = stk[-1][2] + cur * (i - stk[-1][1])
                ans += cnt
                stk.append((cur, i, cnt))
        return ans

func numSubmat(mat [][]int) (ans int) {
	m, n := len(mat), len(mat[0])
	g := make([][]int, m)
	for i := range g {
		g[i] = make([]int, n)
		for j := range g[i] {
			if mat[i][j] == 1 {
				if j == 0 {
					g[i][j] = 1
				} else {
					g[i][j] = 1 + g[i][j-1]
				}
			}
		}
	}
	for i := range g {
		for j := range g[i] {
			col := 1 << 30
			for k := i; k >= 0 && col > 0; k-- {
				col = min(col, g[k][j])
				ans += col
			}
		}
	}
	return
}


// Solution 2
func numSubmat(mat [][]int) (ans int) {
	m, n := len(mat), len(mat[0])
	g := make([][]int, m)
	for i := range g {
		g[i] = make([]int, n)
		for j := range g[i] {
			if mat[i][j] == 1 {
				if j == 0 {
					g[i][j] = 1
				} else {
					g[i][j] = 1 + g[i][j-1]
				}
			}
		}
	}
	for j := 0; j < n; j++ {
		stk := [][3]int{}
		for i := 0; i < m; i++ {
			cur := g[i][j]
			for len(stk) > 0 && stk[len(stk)-1][0] >= cur {
				stk = stk[:len(stk)-1]
			}
			cnt := cur * (i + 1)
			if len(stk) > 0 {
				cnt = stk[len(stk)-1][2] + cur*(i-stk[len(stk)-1][1])
			}
			ans += cnt
			stk = append(stk, [3]int{cur, i, cnt})
		}
	}
	return
}

function numSubmat(mat: number[][]): number {
    const m = mat.length;
    const n = mat[0].length;
    const g: number[][] = Array.from({ length: m }, () => Array(n).fill(0));

    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            if (mat[i][j]) {
                g[i][j] = j === 0 ? 1 : 1 + g[i][j - 1];
            }
        }
    }

    let ans = 0;
    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            let col = Infinity;
            for (let k = i; k >= 0; k--) {
                col = Math.min(col, g[k][j]);
                ans += col;
            }
        }
    }

    return ans;
}



// Solution 2
function numSubmat(mat: number[][]): number {
    const m = mat.length;
    const n = mat[0].length;
    const g: number[][] = Array.from({ length: m }, () => Array(n).fill(0));
    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            if (mat[i][j]) {
                g[i][j] = j === 0 ? 1 : 1 + g[i][j - 1];
            }
        }
    }
    let ans = 0;
    for (let j = 0; j < n; j++) {
        const stk: number[][] = [];
        for (let i = 0; i < m; i++) {
            const cur = g[i][j];
            while (stk.length > 0 && stk[stk.length - 1][0] >= cur) {
                stk.pop();
            }
            let cnt = cur * (i + 1);
            if (stk.length > 0) {
                const t = stk[stk.length - 1];
                cnt = t[2] + cur * (i - t[1]);
            }
            ans += cnt;
            stk.push([cur, i, cnt]);
        }
    }
    return ans;
}

/**
 * @param {number[][]} mat
 * @return {number}
 */
var numSubmat = function (mat) {
    const m = mat.length;
    const n = mat[0].length;
    const g = Array.from({ length: m }, () => Array(n).fill(0));

    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            if (mat[i][j]) {
                g[i][j] = j === 0 ? 1 : 1 + g[i][j - 1];
            }
        }
    }

    let ans = 0;
    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            let col = Infinity;
            for (let k = i; k >= 0; k--) {
                col = Math.min(col, g[k][j]);
                ans += col;
            }
        }
    }

    return ans;
};



// Solution 2
/**
 * @param {number[][]} mat
 * @return {number}
 */
var numSubmat = function (mat) {
    const m = mat.length;
    const n = mat[0].length;
    const g = Array.from({ length: m }, () => Array(n).fill(0));
    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            if (mat[i][j]) {
                g[i][j] = j === 0 ? 1 : 1 + g[i][j - 1];
            }
        }
    }
    let ans = 0;
    for (let j = 0; j < n; j++) {
        const stk = [];
        for (let i = 0; i < m; i++) {
            const cur = g[i][j];
            while (stk.length > 0 && stk[stk.length - 1][0] >= cur) {
                stk.pop();
            }
            let cnt = cur * (i + 1);
            if (stk.length > 0) {
                const t = stk[stk.length - 1];
                cnt = t[2] + cur * (i - t[1]);
            }
            ans += cnt;
            stk.push([cur, i, cnt]);
        }
    }
    return ans;
};

impl Solution {
    pub fn num_submat(mat: Vec<Vec<i32>>) -> i32 {
        let m = mat.len();
        let n = mat[0].len();
        let mut g = vec![vec![0; n]; m];

        for i in 0..m {
            for j in 0..n {
                if mat[i][j] == 1 {
                    if j == 0 {
                        g[i][j] = 1;
                    } else {
                        g[i][j] = 1 + g[i][j - 1];
                    }
                }
            }
        }

        let mut ans = 0;
        for i in 0..m {
            for j in 0..n {
                let mut col = i32::MAX;
                let mut k = i as i32;
                while k >= 0 && col > 0 {
                    col = col.min(g[k as usize][j]);
                    ans += col;
                    k -= 1;
                }
            }
        }
        ans
    }
}



// Solution 2
impl Solution {
    pub fn num_submat(mat: Vec<Vec<i32>>) -> i32 {
        let m = mat.len();
        let n = mat[0].len();
        let mut g = vec![vec![0; n]; m];
        for i in 0..m {
            for j in 0..n {
                if mat[i][j] == 1 {
                    g[i][j] = if j == 0 { 1 } else { 1 + g[i][j - 1] };
                }
            }
        }
        let mut ans = 0;
        for j in 0..n {
            let mut stk: Vec<(i32, i32, i32)> = Vec::new();
            for i in 0..m {
                let cur = g[i][j];
                while !stk.is_empty() && stk.last().unwrap().0 >= cur {
                    stk.pop();
                }
                let cnt = if stk.is_empty() {
                    cur * (i as i32 + 1)
                } else {
                    let t = stk.last().unwrap();
                    t.2 + cur * (i as i32 - t.1)
                };
                ans += cnt;
                stk.push((cur, i as i32, cnt));
            }
        }
        ans
    }
}

1504 - Count Submatrices With All Ones

1504. Count Submatrices With All Ones

Description

Solutions

Solution 2: Monotonic Stack

All Problems

All Solutions

Welcome to Subscribe On Youtube

1504. Count Submatrices With All Ones

Description

Solutions

Solution 2: Monotonic Stack

All Problems

All Solutions