Welcome to Subscribe On Youtube
1466. Reorder Routes to Make All Paths Lead to the City Zero
Description
There are n cities numbered from 0 to n - 1 and n - 1 roads such that there is only one way to travel between two different cities (this network form a tree). Last year, The ministry of transport decided to orient the roads in one direction because they are too narrow.
Roads are represented by connections where connections[i] = [ai, bi] represents a road from city ai to city bi.
This year, there will be a big event in the capital (city 0), and many people want to travel to this city.
Your task consists of reorienting some roads such that each city can visit the city 0. Return the minimum number of edges changed.
It's guaranteed that each city can reach city 0 after reorder.
Example 1:
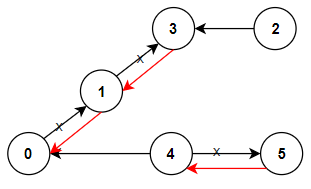
Input: n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]] Output: 3 Explanation: Change the direction of edges show in red such that each node can reach the node 0 (capital).
Example 2:

Input: n = 5, connections = [[1,0],[1,2],[3,2],[3,4]] Output: 2 Explanation: Change the direction of edges show in red such that each node can reach the node 0 (capital).
Example 3:
Input: n = 3, connections = [[1,0],[2,0]] Output: 0
Constraints:
2 <= n <= 5 * 104connections.length == n - 1connections[i].length == 20 <= ai, bi <= n - 1ai != bi
Solutions
Solution 1: DFS
The route map given in the problem has $n$ nodes and $n-1$ edges. If we ignore the direction of the edges, then these $n$ nodes form a tree. The problem requires us to change the direction of some edges so that each node can reach node $0$.
We might as well consider starting from node $0$ and reaching all other nodes. The direction is opposite to the problem description, which means that when we build the graph, for the directed edge $[a, b]$, we should regard it as the directed edge $[b, a]$. That is to say, if it is from $a$ to $b$, we need to change the direction once; if it is from $b$ to $a$, no direction change is needed.
Next, we only need to start from node $0$, search all other nodes, and during the process, if we encounter an edge that needs to change direction, we accumulate the number of direction changes once.
The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes in the problem.
-
class Solution { private List<int[]>[] g; public int minReorder(int n, int[][] connections) { g = new List[n]; Arrays.setAll(g, k -> new ArrayList<>()); for (var e : connections) { int a = e[0], b = e[1]; g[a].add(new int[] {b, 1}); g[b].add(new int[] {a, 0}); } return dfs(0, -1); } private int dfs(int a, int fa) { int ans = 0; for (var e : g[a]) { int b = e[0], c = e[1]; if (b != fa) { ans += c + dfs(b, a); } } return ans; } } -
class Solution { public: int minReorder(int n, vector<vector<int>>& connections) { vector<pair<int, int>> g[n]; for (auto& e : connections) { int a = e[0], b = e[1]; g[a].emplace_back(b, 1); g[b].emplace_back(a, 0); } function<int(int, int)> dfs = [&](int a, int fa) { int ans = 0; for (auto& [b, c] : g[a]) { if (b != fa) { ans += c + dfs(b, a); } } return ans; }; return dfs(0, -1); } }; -
class Solution: def minReorder(self, n: int, connections: List[List[int]]) -> int: def dfs(a: int, fa: int) -> int: return sum(c + dfs(b, a) for b, c in g[a] if b != fa) g = [[] for _ in range(n)] for a, b in connections: g[a].append((b, 1)) g[b].append((a, 0)) return dfs(0, -1) -
func minReorder(n int, connections [][]int) int { g := make([][][2]int, n) for _, e := range connections { a, b := e[0], e[1] g[a] = append(g[a], [2]int{b, 1}) g[b] = append(g[b], [2]int{a, 0}) } var dfs func(int, int) int dfs = func(a, fa int) (ans int) { for _, e := range g[a] { if b, c := e[0], e[1]; b != fa { ans += c + dfs(b, a) } } return } return dfs(0, -1) } -
function minReorder(n: number, connections: number[][]): number { const g: [number, number][][] = Array.from({ length: n }, () => []); for (const [a, b] of connections) { g[a].push([b, 1]); g[b].push([a, 0]); } const dfs = (a: number, fa: number): number => { let ans = 0; for (const [b, c] of g[a]) { if (b !== fa) { ans += c + dfs(b, a); } } return ans; }; return dfs(0, -1); } -
impl Solution { pub fn min_reorder(n: i32, connections: Vec<Vec<i32>>) -> i32 { let mut g: Vec<Vec<(i32, i32)>> = vec![vec![]; n as usize]; for e in connections.iter() { let a = e[0] as usize; let b = e[1] as usize; g[a].push((b as i32, 1)); g[b].push((a as i32, 0)); } fn dfs(a: usize, fa: i32, g: &Vec<Vec<(i32, i32)>>) -> i32 { let mut ans = 0; for &(b, c) in g[a].iter() { if b != fa { ans += c + dfs(b as usize, a as i32, g); } } ans } dfs(0, -1, &g) } }