Welcome to Subscribe On Youtube
1465. Maximum Area of a Piece of Cake After Horizontal and Vertical Cuts
Description
You are given a rectangular cake of size h x w and two arrays of integers horizontalCuts and verticalCuts where:
horizontalCuts[i]is the distance from the top of the rectangular cake to theithhorizontal cut and similarly, andverticalCuts[j]is the distance from the left of the rectangular cake to thejthvertical cut.
Return the maximum area of a piece of cake after you cut at each horizontal and vertical position provided in the arrays horizontalCuts and verticalCuts. Since the answer can be a large number, return this modulo 109 + 7.
Example 1:
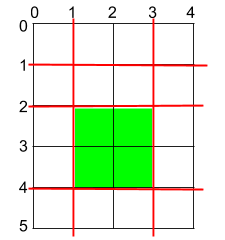
Input: h = 5, w = 4, horizontalCuts = [1,2,4], verticalCuts = [1,3] Output: 4 Explanation: The figure above represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green piece of cake has the maximum area.
Example 2:
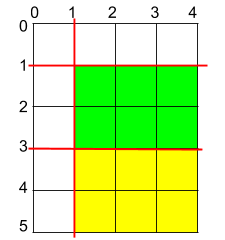
Input: h = 5, w = 4, horizontalCuts = [3,1], verticalCuts = [1] Output: 6 Explanation: The figure above represents the given rectangular cake. Red lines are the horizontal and vertical cuts. After you cut the cake, the green and yellow pieces of cake have the maximum area.
Example 3:
Input: h = 5, w = 4, horizontalCuts = [3], verticalCuts = [3] Output: 9
Constraints:
2 <= h, w <= 1091 <= horizontalCuts.length <= min(h - 1, 105)1 <= verticalCuts.length <= min(w - 1, 105)1 <= horizontalCuts[i] < h1 <= verticalCuts[i] < w- All the elements in
horizontalCutsare distinct. - All the elements in
verticalCutsare distinct.
Solutions
Solution 1: Sorting
We first sort horizontalCuts and verticalCuts separately, and then traverse both arrays to calculate the maximum difference between adjacent elements. We denote these maximum differences as $x$ and $y$, respectively. Finally, we return $x \times y$.
Note that we need to consider the boundary cases, i.e., the first and last elements of horizontalCuts and verticalCuts.
The time complexity is $O(m\log m + n\log n)$, where $m$ and $n$ are the lengths of horizontalCuts and verticalCuts, respectively. The space complexity is $O(\log m + \log n)$.
-
class Solution { public int maxArea(int h, int w, int[] horizontalCuts, int[] verticalCuts) { final int mod = (int) 1e9 + 7; Arrays.sort(horizontalCuts); Arrays.sort(verticalCuts); int m = horizontalCuts.length; int n = verticalCuts.length; long x = Math.max(horizontalCuts[0], h - horizontalCuts[m - 1]); long y = Math.max(verticalCuts[0], w - verticalCuts[n - 1]); for (int i = 1; i < m; ++i) { x = Math.max(x, horizontalCuts[i] - horizontalCuts[i - 1]); } for (int i = 1; i < n; ++i) { y = Math.max(y, verticalCuts[i] - verticalCuts[i - 1]); } return (int) ((x * y) % mod); } } -
class Solution { public: int maxArea(int h, int w, vector<int>& horizontalCuts, vector<int>& verticalCuts) { horizontalCuts.push_back(0); horizontalCuts.push_back(h); verticalCuts.push_back(0); verticalCuts.push_back(w); sort(horizontalCuts.begin(), horizontalCuts.end()); sort(verticalCuts.begin(), verticalCuts.end()); int x = 0, y = 0; for (int i = 1; i < horizontalCuts.size(); ++i) { x = max(x, horizontalCuts[i] - horizontalCuts[i - 1]); } for (int i = 1; i < verticalCuts.size(); ++i) { y = max(y, verticalCuts[i] - verticalCuts[i - 1]); } const int mod = 1e9 + 7; return (1ll * x * y) % mod; } }; -
class Solution: def maxArea( self, h: int, w: int, horizontalCuts: List[int], verticalCuts: List[int] ) -> int: horizontalCuts.extend([0, h]) verticalCuts.extend([0, w]) horizontalCuts.sort() verticalCuts.sort() x = max(b - a for a, b in pairwise(horizontalCuts)) y = max(b - a for a, b in pairwise(verticalCuts)) return (x * y) % (10**9 + 7) -
func maxArea(h int, w int, horizontalCuts []int, verticalCuts []int) int { horizontalCuts = append(horizontalCuts, []int{0, h}...) verticalCuts = append(verticalCuts, []int{0, w}...) sort.Ints(horizontalCuts) sort.Ints(verticalCuts) x, y := 0, 0 const mod int = 1e9 + 7 for i := 1; i < len(horizontalCuts); i++ { x = max(x, horizontalCuts[i]-horizontalCuts[i-1]) } for i := 1; i < len(verticalCuts); i++ { y = max(y, verticalCuts[i]-verticalCuts[i-1]) } return (x * y) % mod } -
function maxArea(h: number, w: number, horizontalCuts: number[], verticalCuts: number[]): number { const mod = 1e9 + 7; horizontalCuts.push(0, h); verticalCuts.push(0, w); horizontalCuts.sort((a, b) => a - b); verticalCuts.sort((a, b) => a - b); let [x, y] = [0, 0]; for (let i = 1; i < horizontalCuts.length; i++) { x = Math.max(x, horizontalCuts[i] - horizontalCuts[i - 1]); } for (let i = 1; i < verticalCuts.length; i++) { y = Math.max(y, verticalCuts[i] - verticalCuts[i - 1]); } return Number((BigInt(x) * BigInt(y)) % BigInt(mod)); } -
impl Solution { pub fn max_area( h: i32, w: i32, mut horizontal_cuts: Vec<i32>, mut vertical_cuts: Vec<i32> ) -> i32 { const MOD: i64 = 1_000_000_007; horizontal_cuts.sort(); vertical_cuts.sort(); let m = horizontal_cuts.len(); let n = vertical_cuts.len(); let mut x = i64::max( horizontal_cuts[0] as i64, (h as i64) - (horizontal_cuts[m - 1] as i64) ); let mut y = i64::max(vertical_cuts[0] as i64, (w as i64) - (vertical_cuts[n - 1] as i64)); for i in 1..m { x = i64::max(x, (horizontal_cuts[i] as i64) - (horizontal_cuts[i - 1] as i64)); } for i in 1..n { y = i64::max(y, (vertical_cuts[i] as i64) - (vertical_cuts[i - 1] as i64)); } ((x * y) % MOD) as i32 } }