Welcome to Subscribe On Youtube
1462. Course Schedule IV
Description
There are a total of numCourses courses you have to take, labeled from 0 to numCourses - 1. You are given an array prerequisites where prerequisites[i] = [ai, bi] indicates that you must take course ai first if you want to take course bi.
- For example, the pair
[0, 1]indicates that you have to take course0before you can take course1.
Prerequisites can also be indirect. If course a is a prerequisite of course b, and course b is a prerequisite of course c, then course a is a prerequisite of course c.
You are also given an array queries where queries[j] = [uj, vj]. For the jth query, you should answer whether course uj is a prerequisite of course vj or not.
Return a boolean array answer, where answer[j] is the answer to the jth query.
Example 1:

Input: numCourses = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]] Output: [false,true] Explanation: The pair [1, 0] indicates that you have to take course 1 before you can take course 0. Course 0 is not a prerequisite of course 1, but the opposite is true.
Example 2:
Input: numCourses = 2, prerequisites = [], queries = [[1,0],[0,1]] Output: [false,false] Explanation: There are no prerequisites, and each course is independent.
Example 3:
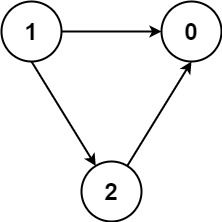
Input: numCourses = 3, prerequisites = [[1,2],[1,0],[2,0]], queries = [[1,0],[1,2]] Output: [true,true]
Constraints:
2 <= numCourses <= 1000 <= prerequisites.length <= (numCourses * (numCourses - 1) / 2)prerequisites[i].length == 20 <= ai, bi <= n - 1ai != bi- All the pairs
[ai, bi]are unique. - The prerequisites graph has no cycles.
1 <= queries.length <= 1040 <= ui, vi <= n - 1ui != vi
Solutions
-
class Solution { public List<Boolean> checkIfPrerequisite(int n, int[][] prerequisites, int[][] queries) { boolean[][] f = new boolean[n][n]; for (var p : prerequisites) { f[p[0]][p[1]] = true; } for (int k = 0; k < n; ++k) { for (int i = 0; i < n; ++i) { for (int j = 0; j < n; ++j) { f[i][j] |= f[i][k] && f[k][j]; } } } List<Boolean> ans = new ArrayList<>(); for (var q : queries) { ans.add(f[q[0]][q[1]]); } return ans; } } -
class Solution { public: vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) { bool f[n][n]; memset(f, false, sizeof(f)); for (auto& p : prerequisites) { f[p[0]][p[1]] = true; } for (int k = 0; k < n; ++k) { for (int i = 0; i < n; ++i) { for (int j = 0; j < n; ++j) { f[i][j] |= (f[i][k] && f[k][j]); } } } vector<bool> ans; for (auto& q : queries) { ans.push_back(f[q[0]][q[1]]); } return ans; } }; -
class Solution: def checkIfPrerequisite( self, n: int, prerequisites: List[List[int]], queries: List[List[int]] ) -> List[bool]: f = [[False] * n for _ in range(n)] for a, b in prerequisites: f[a][b] = True for k in range(n): for i in range(n): for j in range(n): if f[i][k] and f[k][j]: f[i][j] = True return [f[a][b] for a, b in queries] -
func checkIfPrerequisite(n int, prerequisites [][]int, queries [][]int) (ans []bool) { f := make([][]bool, n) for i := range f { f[i] = make([]bool, n) } for _, p := range prerequisites { f[p[0]][p[1]] = true } for k := 0; k < n; k++ { for i := 0; i < n; i++ { for j := 0; j < n; j++ { f[i][j] = f[i][j] || (f[i][k] && f[k][j]) } } } for _, q := range queries { ans = append(ans, f[q[0]][q[1]]) } return } -
function checkIfPrerequisite(n: number, prerequisites: number[][], queries: number[][]): boolean[] { const f = Array.from({ length: n }, () => Array(n).fill(false)); prerequisites.forEach(([a, b]) => (f[a][b] = true)); for (let k = 0; k < n; ++k) { for (let i = 0; i < n; ++i) { for (let j = 0; j < n; ++j) { f[i][j] ||= f[i][k] && f[k][j]; } } } return queries.map(([a, b]) => f[a][b]); }