1457. Pseudo-Palindromic Paths in a Binary Tree

Description

Given a binary tree where node values are digits from 1 to 9. A path in the binary tree is said to be pseudo-palindromic if at least one permutation of the node values in the path is a palindrome.

Return the number of pseudo-palindromic paths going from the root node to leaf nodes.

Example 1:

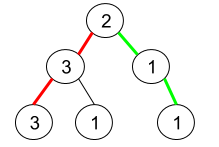
Input: root = [2,3,1,3,1,null,1]
Output: 2 
Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the red path [2,3,3], the green path [2,1,1], and the path [2,3,1]. Among these paths only red path and green path are pseudo-palindromic paths since the red path [2,3,3] can be rearranged in [3,2,3] (palindrome) and the green path [2,1,1] can be rearranged in [1,2,1] (palindrome).

Example 2:

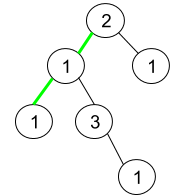
Input: root = [2,1,1,1,3,null,null,null,null,null,1]
Output: 1 
Explanation: The figure above represents the given binary tree. There are three paths going from the root node to leaf nodes: the green path [2,1,1], the path [2,1,3,1], and the path [2,1]. Among these paths only the green path is pseudo-palindromic since [2,1,1] can be rearranged in [1,2,1] (palindrome).

Example 3:

Input: root = [9]
Output: 1

Constraints:

The number of nodes in the tree is in the range [1, 10⁵].
1 <= Node.val <= 9

Solutions

Solution 1: DFS + Bit Manipulation

A path is a pseudo-palindromic path if and only if the number of nodes with odd occurrences in the path is $0$ or $1$.

Since the range of the binary tree node values is from $1$ to $9$, for each path from root to leaf, we can use a $10$-bit binary number $mask$ to represent the occurrence status of the node values in the current path. The $i$th bit of $mask$ is $1$ if the node value $i$ appears an odd number of times in the current path, and $0$ if it appears an even number of times. Therefore, a path is a pseudo-palindromic path if and only if $mask \&(mask - 1) = 0$, where $\&$ represents the bitwise AND operation.

Based on the above analysis, we can use the depth-first search method to calculate the number of paths. We define a function $dfs(root, mask)$, which represents the number of pseudo-palindromic paths starting from the current $root$ node and with the current state $mask$. The answer is $dfs(root, 0)$.

The execution logic of the function $dfs(root, mask)$ is as follows:

If $root$ is null, return $0$;

Otherwise, let $mask = mask \oplus 2^{root.val}$, where $\oplus$ represents the bitwise XOR operation.

If $root$ is a leaf node, return $1$ if $mask \&(mask - 1) = 0$, otherwise return $0$;

If $root$ is not a leaf node, return $dfs(root.left, mask) + dfs(root.right, mask)$.

The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes in the binary tree.

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int pseudoPalindromicPaths(TreeNode root) {
        return dfs(root, 0);
    }

    private int dfs(TreeNode root, int mask) {
        if (root == null) {
            return 0;
        }
        mask ^= 1 << root.val;
        if (root.left == null && root.right == null) {
            return (mask & (mask - 1)) == 0 ? 1 : 0;
        }
        return dfs(root.left, mask) + dfs(root.right, mask);
    }
}

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int pseudoPalindromicPaths(TreeNode* root) {
        function<int(TreeNode*, int)> dfs = [&](TreeNode* root, int mask) {
            if (!root) {
                return 0;
            }
            mask ^= 1 << root->val;
            if (!root->left && !root->right) {
                return (mask & (mask - 1)) == 0 ? 1 : 0;
            }
            return dfs(root->left, mask) + dfs(root->right, mask);
        };
        return dfs(root, 0);
    }
};

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def pseudoPalindromicPaths(self, root: Optional[TreeNode]) -> int:
        def dfs(root: Optional[TreeNode], mask: int):
            if root is None:
                return 0
            mask ^= 1 << root.val
            if root.left is None and root.right is None:
                return int((mask & (mask - 1)) == 0)
            return dfs(root.left, mask) + dfs(root.right, mask)

        return dfs(root, 0)

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func pseudoPalindromicPaths(root *TreeNode) int {
	var dfs func(*TreeNode, int) int
	dfs = func(root *TreeNode, mask int) int {
		if root == nil {
			return 0
		}
		mask ^= 1 << root.Val
		if root.Left == nil && root.Right == nil {
			if mask&(mask-1) == 0 {
				return 1
			}
			return 0
		}
		return dfs(root.Left, mask) + dfs(root.Right, mask)
	}
	return dfs(root, 0)
}

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function pseudoPalindromicPaths(root: TreeNode | null): number {
    const dfs = (root: TreeNode | null, mask: number): number => {
        if (!root) {
            return 0;
        }
        mask ^= 1 << root.val;
        if (!root.left && !root.right) {
            return (mask & (mask - 1)) === 0 ? 1 : 0;
        }
        return dfs(root.left, mask) + dfs(root.right, mask);
    };
    return dfs(root, 0);
}

// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
use std::rc::Rc;
use std::cell::RefCell;

impl Solution {
    pub fn pseudo_palindromic_paths(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
        fn dfs(root: Option<Rc<RefCell<TreeNode>>>, mask: i32) -> i32 {
            if let Some(node) = root {
                let mut mask = mask;
                let val = node.borrow().val;
                mask ^= 1 << val;

                if node.borrow().left.is_none() && node.borrow().right.is_none() {
                    return if (mask & (mask - 1)) == 0 { 1 } else { 0 };
                }

                return (
                    dfs(node.borrow().left.clone(), mask) + dfs(node.borrow().right.clone(), mask)
                );
            }
            0
        }

        dfs(root, 0)
    }
}

1457 - Pseudo-Palindromic Paths in a Binary Tree

1457. Pseudo-Palindromic Paths in a Binary Tree

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

1457. Pseudo-Palindromic Paths in a Binary Tree

Description

Solutions

All Problems

All Solutions