Welcome to Subscribe On Youtube

1391. Check if There is a Valid Path in a Grid

Description

You are given an m x n grid. Each cell of grid represents a street. The street of grid[i][j] can be:

• 1 which means a street connecting the left cell and the right cell.
• 2 which means a street connecting the upper cell and the lower cell.
• 3 which means a street connecting the left cell and the lower cell.
• 4 which means a street connecting the right cell and the lower cell.
• 5 which means a street connecting the left cell and the upper cell.
• 6 which means a street connecting the right cell and the upper cell.

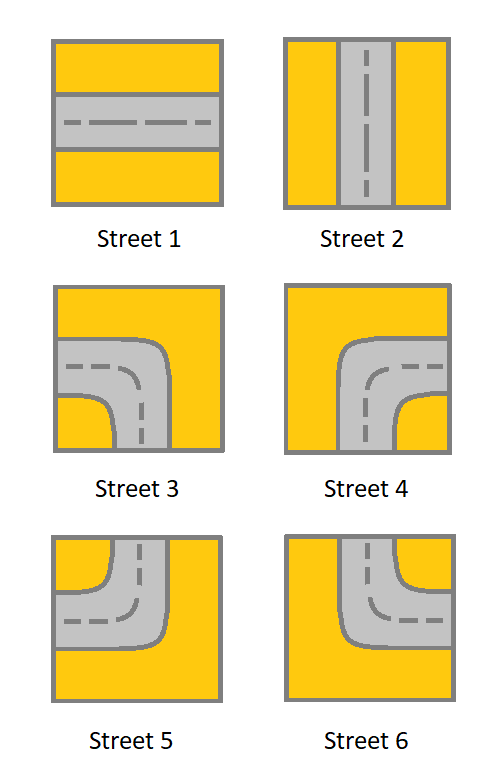
You will initially start at the street of the upper-left cell (0, 0). A valid path in the grid is a path that starts from the upper left cell (0, 0) and ends at the bottom-right cell (m - 1, n - 1). The path should only follow the streets.

Notice that you are not allowed to change any street.

Return true if there is a valid path in the grid or false otherwise.

 

Example 1:

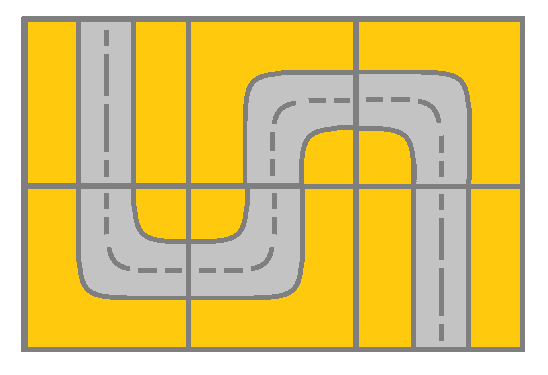
Input: grid = [[2,4,3],[6,5,2]]
Output: true
Explanation: As shown you can start at cell (0, 0) and visit all the cells of the grid to reach (m - 1, n - 1).

Example 2:

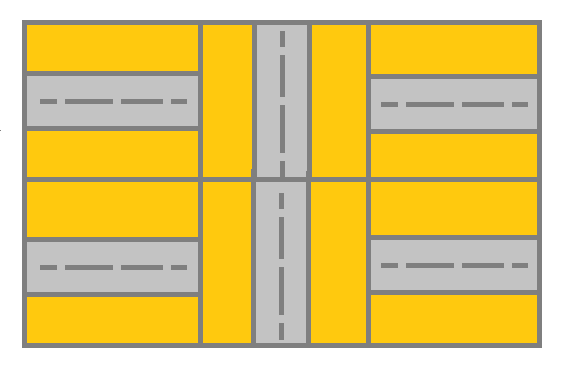
Input: grid = [[1,2,1],[1,2,1]]
Output: false
Explanation: As shown you the street at cell (0, 0) is not connected with any street of any other cell and you will get stuck at cell (0, 0)

Example 3:

Input: grid = [[1,1,2]]
Output: false
Explanation: You will get stuck at cell (0, 1) and you cannot reach cell (0, 2).

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 300
• 1 <= grid[i][j] <= 6

Solutions

Union find.

• Java
• C++
• Python
• Go

• class Solution {
      private int[] p;
      private int[][] grid;
      private int m;
      private int n;
  
      public boolean hasValidPath(int[][] grid) {
          this.grid = grid;
          m = grid.length;
          n = grid[0].length;
          p = new int[m * n];
          for (int i = 0; i < p.length; ++i) {
              p[i] = i;
          }
          for (int i = 0; i < m; ++i) {
              for (int j = 0; j < n; ++j) {
                  int e = grid[i][j];
                  if (e == 1) {
                      left(i, j);
                      right(i, j);
                  } else if (e == 2) {
                      up(i, j);
                      down(i, j);
                  } else if (e == 3) {
                      left(i, j);
                      down(i, j);
                  } else if (e == 4) {
                      right(i, j);
                      down(i, j);
                  } else if (e == 5) {
                      left(i, j);
                      up(i, j);
                  } else {
                      right(i, j);
                      up(i, j);
                  }
              }
          }
          return find(0) == find(m * n - 1);
      }
  
      private int find(int x) {
          if (p[x] != x) {
              p[x] = find(p[x]);
          }
          return p[x];
      }
  
      private void left(int i, int j) {
          if (j > 0 && (grid[i][j - 1] == 1 || grid[i][j - 1] == 4 || grid[i][j - 1] == 6)) {
              p[find(i * n + j)] = find(i * n + j - 1);
          }
      }
  
      private void right(int i, int j) {
          if (j < n - 1 && (grid[i][j + 1] == 1 || grid[i][j + 1] == 3 || grid[i][j + 1] == 5)) {
              p[find(i * n + j)] = find(i * n + j + 1);
          }
      }
  
      private void up(int i, int j) {
          if (i > 0 && (grid[i - 1][j] == 2 || grid[i - 1][j] == 3 || grid[i - 1][j] == 4)) {
              p[find(i * n + j)] = find((i - 1) * n + j);
          }
      }
  
      private void down(int i, int j) {
          if (i < m - 1 && (grid[i + 1][j] == 2 || grid[i + 1][j] == 5 || grid[i + 1][j] == 6)) {
              p[find(i * n + j)] = find((i + 1) * n + j);
          }
      }
  }
  

• class Solution {
  public:
      vector<int> p;
  
      bool hasValidPath(vector<vector<int>>& grid) {
          int m = grid.size();
          int n = grid[0].size();
          p.resize(m * n);
          for (int i = 0; i < p.size(); ++i) p[i] = i;
          auto left = [&](int i, int j) {
              if (j > 0 && (grid[i][j - 1] == 1 || grid[i][j - 1] == 4 || grid[i][j - 1] == 6)) {
                  p[find(i * n + j)] = find(i * n + j - 1);
              }
          };
          auto right = [&](int i, int j) {
              if (j < n - 1 && (grid[i][j + 1] == 1 || grid[i][j + 1] == 3 || grid[i][j + 1] == 5)) {
                  p[find(i * n + j)] = find(i * n + j + 1);
              }
          };
          auto up = [&](int i, int j) {
              if (i > 0 && (grid[i - 1][j] == 2 || grid[i - 1][j] == 3 || grid[i - 1][j] == 4)) {
                  p[find(i * n + j)] = find((i - 1) * n + j);
              }
          };
          auto down = [&](int i, int j) {
              if (i < m - 1 && (grid[i + 1][j] == 2 || grid[i + 1][j] == 5 || grid[i + 1][j] == 6)) {
                  p[find(i * n + j)] = find((i + 1) * n + j);
              }
          };
          for (int i = 0; i < m; ++i) {
              for (int j = 0; j < n; ++j) {
                  int e = grid[i][j];
                  if (e == 1) {
                      left(i, j);
                      right(i, j);
                  } else if (e == 2) {
                      up(i, j);
                      down(i, j);
                  } else if (e == 3) {
                      left(i, j);
                      down(i, j);
                  } else if (e == 4) {
                      right(i, j);
                      down(i, j);
                  } else if (e == 5) {
                      left(i, j);
                      up(i, j);
                  } else {
                      right(i, j);
                      up(i, j);
                  }
              }
          }
          return find(0) == find(m * n - 1);
      }
  
      int find(int x) {
          if (p[x] != x) p[x] = find(p[x]);
          return p[x];
      }
  };
  

• class Solution:
      def hasValidPath(self, grid: List[List[int]]) -> bool:
          m, n = len(grid), len(grid[0])
          p = list(range(m * n))
  
          def find(x):
              if p[x] != x:
                  p[x] = find(p[x])
              return p[x]
  
          def left(i, j):
              if j > 0 and grid[i][j - 1] in (1, 4, 6):
                  p[find(i * n + j)] = find(i * n + j - 1)
  
          def right(i, j):
              if j < n - 1 and grid[i][j + 1] in (1, 3, 5):
                  p[find(i * n + j)] = find(i * n + j + 1)
  
          def up(i, j):
              if i > 0 and grid[i - 1][j] in (2, 3, 4):
                  p[find(i * n + j)] = find((i - 1) * n + j)
  
          def down(i, j):
              if i < m - 1 and grid[i + 1][j] in (2, 5, 6):
                  p[find(i * n + j)] = find((i + 1) * n + j)
  
          for i in range(m):
              for j in range(n):
                  e = grid[i][j]
                  if e == 1:
                      left(i, j)
                      right(i, j)
                  elif e == 2:
                      up(i, j)
                      down(i, j)
                  elif e == 3:
                      left(i, j)
                      down(i, j)
                  elif e == 4:
                      right(i, j)
                      down(i, j)
                  elif e == 5:
                      left(i, j)
                      up(i, j)
                  else:
                      right(i, j)
                      up(i, j)
          return find(0) == find(m * n - 1)
  
  

• func hasValidPath(grid [][]int) bool {
  	m, n := len(grid), len(grid[0])
  	p := make([]int, m*n)
  	for i := range p {
  		p[i] = i
  	}
  	var find func(x int) int
  	find = func(x int) int {
  		if p[x] != x {
  			p[x] = find(p[x])
  		}
  		return p[x]
  	}
  	left := func(i, j int) {
  		if j > 0 && (grid[i][j-1] == 1 || grid[i][j-1] == 4 || grid[i][j-1] == 6) {
  			p[find(i*n+j)] = find(i*n + j - 1)
  		}
  	}
  	right := func(i, j int) {
  		if j < n-1 && (grid[i][j+1] == 1 || grid[i][j+1] == 3 || grid[i][j+1] == 5) {
  			p[find(i*n+j)] = find(i*n + j + 1)
  		}
  	}
  	up := func(i, j int) {
  		if i > 0 && (grid[i-1][j] == 2 || grid[i-1][j] == 3 || grid[i-1][j] == 4) {
  			p[find(i*n+j)] = find((i-1)*n + j)
  		}
  	}
  	down := func(i, j int) {
  		if i < m-1 && (grid[i+1][j] == 2 || grid[i+1][j] == 5 || grid[i+1][j] == 6) {
  			p[find(i*n+j)] = find((i+1)*n + j)
  		}
  	}
  	for i, row := range grid {
  		for j, e := range row {
  			if e == 1 {
  				left(i, j)
  				right(i, j)
  			} else if e == 2 {
  				up(i, j)
  				down(i, j)
  			} else if e == 3 {
  				left(i, j)
  				down(i, j)
  			} else if e == 4 {
  				right(i, j)
  				down(i, j)
  			} else if e == 5 {
  				left(i, j)
  				up(i, j)
  			} else {
  				right(i, j)
  				up(i, j)
  			}
  		}
  	}
  	return find(0) == find(m*n-1)
  }
  

All Problems

All Solutions