Welcome to Subscribe On Youtube
1386. Cinema Seat Allocation
Description
A cinema has n rows of seats, numbered from 1 to n and there are ten seats in each row, labelled from 1 to 10 as shown in the figure above.
Given the array reservedSeats containing the numbers of seats already reserved, for example, reservedSeats[i] = [3,8] means the seat located in row 3 and labelled with 8 is already reserved.
Return the maximum number of four-person groups you can assign on the cinema seats. A four-person group occupies four adjacent seats in one single row. Seats across an aisle (such as [3,3] and [3,4]) are not considered to be adjacent, but there is an exceptional case on which an aisle split a four-person group, in that case, the aisle split a four-person group in the middle, which means to have two people on each side.
Example 1:
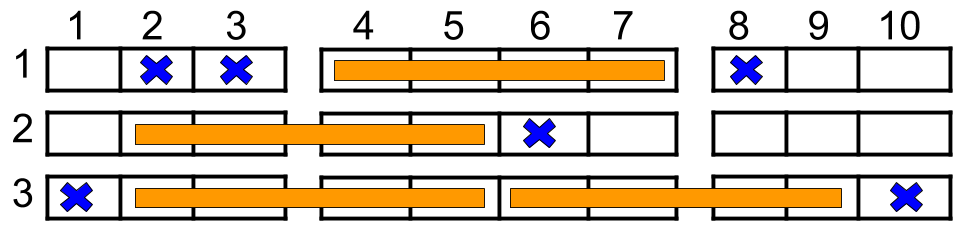
Input: n = 3, reservedSeats = [[1,2],[1,3],[1,8],[2,6],[3,1],[3,10]] Output: 4 Explanation: The figure above shows the optimal allocation for four groups, where seats mark with blue are already reserved and contiguous seats mark with orange are for one group.
Example 2:
Input: n = 2, reservedSeats = [[2,1],[1,8],[2,6]] Output: 2
Example 3:
Input: n = 4, reservedSeats = [[4,3],[1,4],[4,6],[1,7]] Output: 4
Constraints:
1 <= n <= 10^91 <= reservedSeats.length <= min(10*n, 10^4)reservedSeats[i].length == 21 <= reservedSeats[i][0] <= n1 <= reservedSeats[i][1] <= 10- All
reservedSeats[i]are distinct.
Solutions
Solution 1: Hash Table + Bit Manipulation
We use a hash table $d$ to store all the reserved seats, where the key is the row number, and the value is the state of the reserved seats in that row, i.e., a binary number. The $j$-th bit being $1$ means the $j$-th seat is reserved, and $0$ means the $j$-th seat is not reserved.
We traverse $reservedSeats$, for each seat $(i, j)$, we add the state of the $j$-th seat (corresponding to the $10-j$ bit in the lower bits) to $d[i]$.
For rows that do not appear in the hash table $d$, we can arrange $2$ families arbitrarily, so the initial answer is $(n - len(d)) \times 2$.
Next, we traverse the state of each row in the hash table. For each row, we try to arrange the situations $1234, 5678, 3456$ in turn. If a situation can be arranged, we add $1$ to the answer.
After the traversal, we get the final answer.
The time complexity is $O(m)$, and the space complexity is $O(m)$. Where $m$ is the length of $reservedSeats$.
-
class Solution { public int maxNumberOfFamilies(int n, int[][] reservedSeats) { Map<Integer, Integer> d = new HashMap<>(); for (var e : reservedSeats) { int i = e[0], j = e[1]; d.merge(i, 1 << (10 - j), (x, y) -> x | y); } int[] masks = {0b0111100000, 0b0000011110, 0b0001111000}; int ans = (n - d.size()) * 2; for (int x : d.values()) { for (int mask : masks) { if ((x & mask) == 0) { x |= mask; ++ans; } } } return ans; } } -
class Solution { public: int maxNumberOfFamilies(int n, vector<vector<int>>& reservedSeats) { unordered_map<int, int> d; for (auto& e : reservedSeats) { int i = e[0], j = e[1]; d[i] |= 1 << (10 - j); } int masks[3] = {0b0111100000, 0b0000011110, 0b0001111000}; int ans = (n - d.size()) * 2; for (auto& [_, x] : d) { for (int& mask : masks) { if ((x & mask) == 0) { x |= mask; ++ans; } } } return ans; } }; -
class Solution: def maxNumberOfFamilies(self, n: int, reservedSeats: List[List[int]]) -> int: d = defaultdict(int) for i, j in reservedSeats: d[i] |= 1 << (10 - j) masks = (0b0111100000, 0b0000011110, 0b0001111000) ans = (n - len(d)) * 2 for x in d.values(): for mask in masks: if (x & mask) == 0: x |= mask ans += 1 return ans -
func maxNumberOfFamilies(n int, reservedSeats [][]int) int { d := map[int]int{} for _, e := range reservedSeats { i, j := e[0], e[1] d[i] |= 1 << (10 - j) } ans := (n - len(d)) * 2 masks := [3]int{0b0111100000, 0b0000011110, 0b0001111000} for _, x := range d { for _, mask := range masks { if x&mask == 0 { x |= mask ans++ } } } return ans } -
function maxNumberOfFamilies(n: number, reservedSeats: number[][]): number { const d: Map<number, number> = new Map(); for (const [i, j] of reservedSeats) { d.set(i, (d.get(i) ?? 0) | (1 << (10 - j))); } let ans = (n - d.size) << 1; const masks = [0b0111100000, 0b0000011110, 0b0001111000]; for (let [_, x] of d) { for (const mask of masks) { if ((x & mask) === 0) { x |= mask; ++ans; } } } return ans; }