Welcome to Subscribe On Youtube
1349. Maximum Students Taking Exam
Description
Given a m * n matrix seats that represent seats distributions in a classroom. If a seat is broken, it is denoted by '#' character otherwise it is denoted by a '.' character.
Students can see the answers of those sitting next to the left, right, upper left and upper right, but he cannot see the answers of the student sitting directly in front or behind him. Return the maximum number of students that can take the exam together without any cheating being possible.
Students must be placed in seats in good condition.
Example 1:
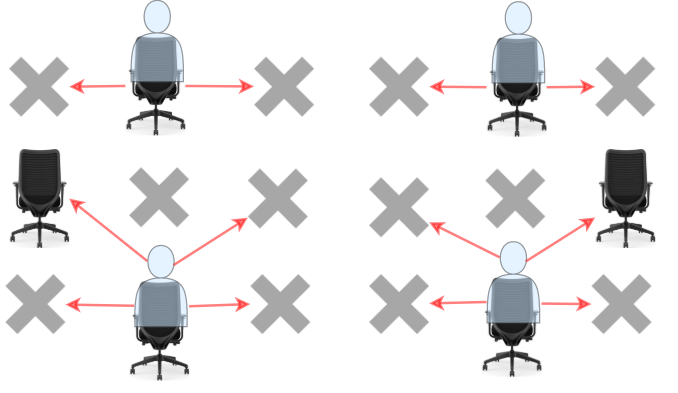
Input: seats = [["#",".","#","#",".","#"], [".","#","#","#","#","."], ["#",".","#","#",".","#"]] Output: 4 Explanation: Teacher can place 4 students in available seats so they don't cheat on the exam.
Example 2:
Input: seats = [[".","#"], ["#","#"], ["#","."], ["#","#"], [".","#"]] Output: 3 Explanation: Place all students in available seats.
Example 3:
Input: seats = [["#",".",".",".","#"], [".","#",".","#","."], [".",".","#",".","."], [".","#",".","#","."], ["#",".",".",".","#"]] Output: 10 Explanation: Place students in available seats in column 1, 3 and 5.
Constraints:
seatscontains only characters'.' and'#'.m == seats.lengthn == seats[i].length1 <= m <= 81 <= n <= 8
Solutions
Solution 1: State Compression + Memoization Search
We notice that each seat has two states: selectable and non-selectable. Therefore, we can use a binary number to represent the seat state of each row, where $1$ represents selectable, and $0$ represents non-selectable. For example, for the first row in Example 1, we can represent it as $010010$. Therefore, we convert the initial seats into a one-dimensional array $ss$, where $ss[i]$ represents the seat state of the $i$th row.
Next, we design a function $dfs(seat, i)$, which represents the maximum number of students that can be accommodated starting from the $i$th row, and the seat state of the current row is $seat$.
We can enumerate all the seat selection states $mask$ of the $i$th row, and judge whether $mask$ meets the following conditions:
- The state $mask$ cannot select seats outside of $seat$;
- The state $mask$ cannot select adjacent seats.
If the conditions are met, we calculate the number of seats selected in the current row $cnt$. If it is the last row, update the return value of the function, that is, $ans = \max(ans, cnt)$. Otherwise, we continue to recursively solve the maximum number of the next row. The seat state of the next row is $nxt = ss[i + 1]$, and we need to exclude the left and right sides of the selected seats in the current row. Then we recursively solve the maximum number of the next row, that is, $ans = \max(ans, cnt + dfs(nxt, i + 1))$.
Finally, we return $ans$ as the return value of the function.
To avoid repeated calculations, we can use memoization search to save the return value of the function $dfs(seat, i)$ in a two-dimensional array $f$, where $f[seat][i]$ represents the maximum number of students that can be accommodated starting from the $i$th row, and the seat state of the current row is $seat$.
The time complexity is $O(4^n \times n \times m)$, and the space complexity is $O(2^n \times m)$. Where $m$ and $n$ are the number of rows and columns of the seats, respectively.
-
class Solution { private Integer[][] f; private int n; private int[] ss; public int maxStudents(char[][] seats) { int m = seats.length; n = seats[0].length; ss = new int[m]; f = new Integer[1 << n][m]; for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { if (seats[i][j] == '.') { ss[i] |= 1 << j; } } } return dfs(ss[0], 0); } private int dfs(int seat, int i) { if (f[seat][i] != null) { return f[seat][i]; } int ans = 0; for (int mask = 0; mask < 1 << n; ++mask) { if ((seat | mask) != seat || (mask & (mask << 1)) != 0) { continue; } int cnt = Integer.bitCount(mask); if (i == ss.length - 1) { ans = Math.max(ans, cnt); } else { int nxt = ss[i + 1]; nxt &= ~(mask << 1); nxt &= ~(mask >> 1); ans = Math.max(ans, cnt + dfs(nxt, i + 1)); } } return f[seat][i] = ans; } } -
class Solution { public: int maxStudents(vector<vector<char>>& seats) { int m = seats.size(); int n = seats[0].size(); vector<int> ss(m); vector<vector<int>> f(1 << n, vector<int>(m, -1)); for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { if (seats[i][j] == '.') { ss[i] |= 1 << j; } } } function<int(int, int)> dfs = [&](int seat, int i) -> int { if (f[seat][i] != -1) { return f[seat][i]; } int ans = 0; for (int mask = 0; mask < 1 << n; ++mask) { if ((seat | mask) != seat || (mask & (mask << 1)) != 0) { continue; } int cnt = __builtin_popcount(mask); if (i == m - 1) { ans = max(ans, cnt); } else { int nxt = ss[i + 1]; nxt &= ~(mask >> 1); nxt &= ~(mask << 1); ans = max(ans, cnt + dfs(nxt, i + 1)); } } return f[seat][i] = ans; }; return dfs(ss[0], 0); } }; -
class Solution: def maxStudents(self, seats: List[List[str]]) -> int: def f(seat: List[str]) -> int: mask = 0 for i, c in enumerate(seat): if c == '.': mask |= 1 << i return mask @cache def dfs(seat: int, i: int) -> int: ans = 0 for mask in range(1 << n): if (seat | mask) != seat or (mask & (mask << 1)): continue cnt = mask.bit_count() if i == len(ss) - 1: ans = max(ans, cnt) else: nxt = ss[i + 1] nxt &= ~(mask << 1) nxt &= ~(mask >> 1) ans = max(ans, cnt + dfs(nxt, i + 1)) return ans n = len(seats[0]) ss = [f(s) for s in seats] return dfs(ss[0], 0) -
func maxStudents(seats [][]byte) int { m, n := len(seats), len(seats[0]) ss := make([]int, m) f := make([][]int, 1<<n) for i, seat := range seats { for j, c := range seat { if c == '.' { ss[i] |= 1 << j } } } for i := range f { f[i] = make([]int, m) for j := range f[i] { f[i][j] = -1 } } var dfs func(int, int) int dfs = func(seat, i int) int { if f[seat][i] != -1 { return f[seat][i] } ans := 0 for mask := 0; mask < 1<<n; mask++ { if (seat|mask) != seat || (mask&(mask<<1)) != 0 { continue } cnt := bits.OnesCount(uint(mask)) if i == m-1 { ans = max(ans, cnt) } else { nxt := ss[i+1] & ^(mask >> 1) & ^(mask << 1) ans = max(ans, cnt+dfs(nxt, i+1)) } } f[seat][i] = ans return ans } return dfs(ss[0], 0) } -
function maxStudents(seats: string[][]): number { const m: number = seats.length; const n: number = seats[0].length; const ss: number[] = Array(m).fill(0); const f: number[][] = Array.from({ length: 1 << n }, () => Array(m).fill(-1)); for (let i = 0; i < m; ++i) { for (let j = 0; j < n; ++j) { if (seats[i][j] === '.') { ss[i] |= 1 << j; } } } const dfs = (seat: number, i: number): number => { if (f[seat][i] !== -1) { return f[seat][i]; } let ans: number = 0; for (let mask = 0; mask < 1 << n; ++mask) { if ((seat | mask) !== seat || (mask & (mask << 1)) !== 0) { continue; } const cnt: number = mask.toString(2).split('1').length - 1; if (i === m - 1) { ans = Math.max(ans, cnt); } else { let nxt: number = ss[i + 1]; nxt &= ~(mask >> 1); nxt &= ~(mask << 1); ans = Math.max(ans, cnt + dfs(nxt, i + 1)); } } return (f[seat][i] = ans); }; return dfs(ss[0], 0); }