Welcome to Subscribe On Youtube
1326. Minimum Number of Taps to Open to Water a Garden
Description
There is a one-dimensional garden on the x-axis. The garden starts at the point 0 and ends at the point n. (i.e., the length of the garden is n).
There are n + 1 taps located at points [0, 1, ..., n] in the garden.
Given an integer n and an integer array ranges of length n + 1 where ranges[i] (0-indexed) means the i-th tap can water the area [i - ranges[i], i + ranges[i]] if it was open.
Return the minimum number of taps that should be open to water the whole garden, If the garden cannot be watered return -1.
Example 1:
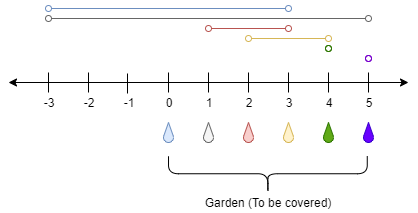
Input: n = 5, ranges = [3,4,1,1,0,0] Output: 1 Explanation: The tap at point 0 can cover the interval [-3,3] The tap at point 1 can cover the interval [-3,5] The tap at point 2 can cover the interval [1,3] The tap at point 3 can cover the interval [2,4] The tap at point 4 can cover the interval [4,4] The tap at point 5 can cover the interval [5,5] Opening Only the second tap will water the whole garden [0,5]
Example 2:
Input: n = 3, ranges = [0,0,0,0] Output: -1 Explanation: Even if you activate all the four taps you cannot water the whole garden.
Constraints:
1 <= n <= 104ranges.length == n + 10 <= ranges[i] <= 100
Solutions
-
class Solution { public int minTaps(int n, int[] ranges) { int[] last = new int[n + 1]; for (int i = 0; i < n + 1; ++i) { int l = Math.max(0, i - ranges[i]), r = i + ranges[i]; last[l] = Math.max(last[l], r); } int ans = 0, mx = 0, pre = 0; for (int i = 0; i < n; ++i) { mx = Math.max(mx, last[i]); if (mx <= i) { return -1; } if (pre == i) { ++ans; pre = mx; } } return ans; } } -
class Solution { public: int minTaps(int n, vector<int>& ranges) { vector<int> last(n + 1); for (int i = 0; i < n + 1; ++i) { int l = max(0, i - ranges[i]), r = i + ranges[i]; last[l] = max(last[l], r); } int ans = 0, mx = 0, pre = 0; for (int i = 0; i < n; ++i) { mx = max(mx, last[i]); if (mx <= i) { return -1; } if (pre == i) { ++ans; pre = mx; } } return ans; } }; -
class Solution: def minTaps(self, n: int, ranges: List[int]) -> int: last = [0] * (n + 1) for i, x in enumerate(ranges): l, r = max(0, i - x), i + x last[l] = max(last[l], r) ans = mx = pre = 0 for i in range(n): mx = max(mx, last[i]) if mx <= i: return -1 if pre == i: ans += 1 pre = mx return ans -
func minTaps(n int, ranges []int) (ans int) { last := make([]int, n+1) for i, x := range ranges { l, r := max(0, i-x), i+x last[l] = max(last[l], r) } var pre, mx int for i, j := range last[:n] { mx = max(mx, j) if mx <= i { return -1 } if pre == i { ans++ pre = mx } } return } -
function minTaps(n: number, ranges: number[]): number { const last = new Array(n + 1).fill(0); for (let i = 0; i < n + 1; ++i) { const l = Math.max(0, i - ranges[i]); const r = i + ranges[i]; last[l] = Math.max(last[l], r); } let ans = 0; let mx = 0; let pre = 0; for (let i = 0; i < n; ++i) { mx = Math.max(mx, last[i]); if (mx <= i) { return -1; } if (pre == i) { ++ans; pre = mx; } } return ans; } -
impl Solution { #[allow(dead_code)] pub fn min_taps(n: i32, ranges: Vec<i32>) -> i32 { let mut last = vec![0; (n + 1) as usize]; let mut ans = 0; let mut mx = 0; let mut pre = 0; // Initialize the last vector for (i, &r) in ranges.iter().enumerate() { if (i as i32) - r >= 0 { last[((i as i32) - r) as usize] = std::cmp::max( last[((i as i32) - r) as usize], (i as i32) + r ); } else { last[0] = std::cmp::max(last[0], (i as i32) + r); } } for i in 0..n as usize { mx = std::cmp::max(mx, last[i]); if mx <= (i as i32) { return -1; } if pre == (i as i32) { ans += 1; pre = mx; } } ans } }