Welcome to Subscribe On Youtube
1275. Find Winner on a Tic Tac Toe Game
Description
Tic-tac-toe is played by two players A and B on a 3 x 3 grid. The rules of Tic-Tac-Toe are:
- Players take turns placing characters into empty squares
' '. - The first player
Aalways places'X'characters, while the second playerBalways places'O'characters. 'X'and'O'characters are always placed into empty squares, never on filled ones.- The game ends when there are three of the same (non-empty) character filling any row, column, or diagonal.
- The game also ends if all squares are non-empty.
- No more moves can be played if the game is over.
Given a 2D integer array moves where moves[i] = [rowi, coli] indicates that the ith move will be played on grid[rowi][coli]. return the winner of the game if it exists (A or B). In case the game ends in a draw return "Draw". If there are still movements to play return "Pending".
You can assume that moves is valid (i.e., it follows the rules of Tic-Tac-Toe), the grid is initially empty, and A will play first.
Example 1:
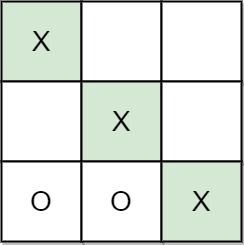
Input: moves = [[0,0],[2,0],[1,1],[2,1],[2,2]] Output: "A" Explanation: A wins, they always play first.
Example 2:
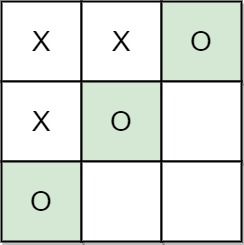
Input: moves = [[0,0],[1,1],[0,1],[0,2],[1,0],[2,0]] Output: "B" Explanation: B wins.
Example 3:

Input: moves = [[0,0],[1,1],[2,0],[1,0],[1,2],[2,1],[0,1],[0,2],[2,2]] Output: "Draw" Explanation: The game ends in a draw since there are no moves to make.
Constraints:
1 <= moves.length <= 9moves[i].length == 20 <= rowi, coli <= 2- There are no repeated elements on
moves. movesfollow the rules of tic tac toe.
Solutions
Solution 1: Determine if the last player to move can win
Since all moves are valid, that is, there is no situation where a person continues to play after someone has won. Therefore, we only need to determine whether the last player to move can win.
We use an array cnt of length $8$ to record the number of moves in rows, columns, and diagonals. Where $cnt[0, 1, 2]$ represent the number of moves in the $0, 1, 2$ rows respectively, and $cnt[3, 4, 5]$ represent the number of moves in the $0, 1, 2$ columns respectively. Additionally, $cnt[6]$ and $cnt[7]$ represent the number of moves on the two diagonals respectively. During the game, if a player makes $3$ moves in a row, column, or diagonal, that player wins.
If the last player to move does not win, then we determine whether the board is full. If it is full, it is a draw; otherwise, the game is not over yet.
The time complexity is $O(n)$, and the space complexity is $O(n)$. Where $n$ is the length of moves.
-
class Solution { public String tictactoe(int[][] moves) { int n = moves.length; int[] cnt = new int[8]; for (int k = n - 1; k >= 0; k -= 2) { int i = moves[k][0], j = moves[k][1]; cnt[i]++; cnt[j + 3]++; if (i == j) { cnt[6]++; } if (i + j == 2) { cnt[7]++; } if (cnt[i] == 3 || cnt[j + 3] == 3 || cnt[6] == 3 || cnt[7] == 3) { return k % 2 == 0 ? "A" : "B"; } } return n == 9 ? "Draw" : "Pending"; } } -
class Solution { public: string tictactoe(vector<vector<int>>& moves) { int n = moves.size(); int cnt[8]{}; for (int k = n - 1; k >= 0; k -= 2) { int i = moves[k][0], j = moves[k][1]; cnt[i]++; cnt[j + 3]++; if (i == j) { cnt[6]++; } if (i + j == 2) { cnt[7]++; } if (cnt[i] == 3 || cnt[j + 3] == 3 || cnt[6] == 3 || cnt[7] == 3) { return k % 2 == 0 ? "A" : "B"; } } return n == 9 ? "Draw" : "Pending"; } }; -
class Solution: def tictactoe(self, moves: List[List[int]]) -> str: n = len(moves) cnt = [0] * 8 for k in range(n - 1, -1, -2): i, j = moves[k] cnt[i] += 1 cnt[j + 3] += 1 if i == j: cnt[6] += 1 if i + j == 2: cnt[7] += 1 if any(v == 3 for v in cnt): return "B" if k & 1 else "A" return "Draw" if n == 9 else "Pending" -
func tictactoe(moves [][]int) string { n := len(moves) cnt := [8]int{} for k := n - 1; k >= 0; k -= 2 { i, j := moves[k][0], moves[k][1] cnt[i]++ cnt[j+3]++ if i == j { cnt[6]++ } if i+j == 2 { cnt[7]++ } if cnt[i] == 3 || cnt[j+3] == 3 || cnt[6] == 3 || cnt[7] == 3 { if k%2 == 0 { return "A" } return "B" } } if n == 9 { return "Draw" } return "Pending" } -
function tictactoe(moves: number[][]): string { const n = moves.length; const cnt = new Array(8).fill(0); for (let k = n - 1; k >= 0; k -= 2) { const [i, j] = moves[k]; cnt[i]++; cnt[j + 3]++; if (i == j) { cnt[6]++; } if (i + j == 2) { cnt[7]++; } if (cnt[i] == 3 || cnt[j + 3] == 3 || cnt[6] == 3 || cnt[7] == 3) { return k % 2 == 0 ? 'A' : 'B'; } } return n == 9 ? 'Draw' : 'Pending'; }