Welcome to Subscribe On Youtube
1274. Number of Ships in a Rectangle
Description
(This problem is an interactive problem.)
Each ship is located at an integer point on the sea represented by a cartesian plane, and each integer point may contain at most 1 ship.
You have a function Sea.hasShips(topRight, bottomLeft) which takes two points as arguments and returns true If there is at least one ship in the rectangle represented by the two points, including on the boundary.
Given two points: the top right and bottom left corners of a rectangle, return the number of ships present in that rectangle. It is guaranteed that there are at most 10 ships in that rectangle.
Submissions making more than 400 calls to hasShips will be judged Wrong Answer. Also, any solutions that attempt to circumvent the judge will result in disqualification.
Example :
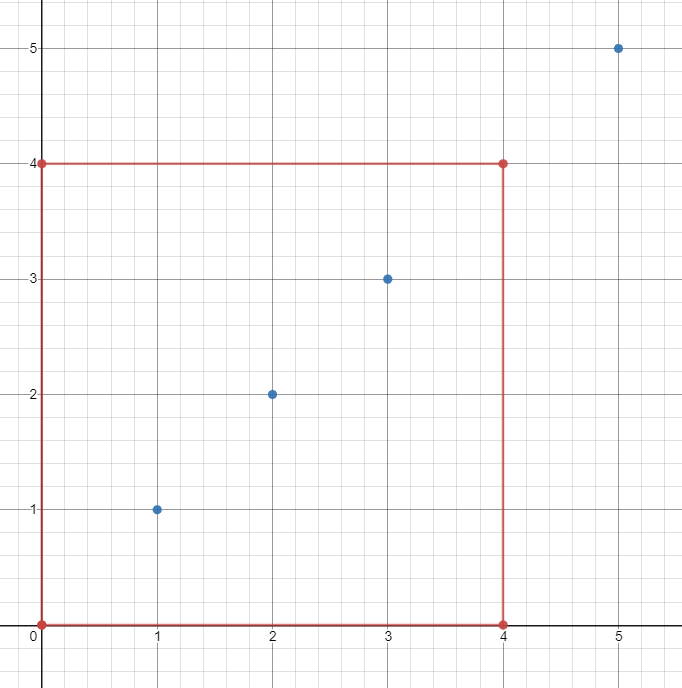
Input: ships = [[1,1],[2,2],[3,3],[5,5]], topRight = [4,4], bottomLeft = [0,0] Output: 3 Explanation: From [0,0] to [4,4] we can count 3 ships within the range.
Example 2:
Input: ans = [[1,1],[2,2],[3,3]], topRight = [1000,1000], bottomLeft = [0,0] Output: 3
Constraints:
- On the input
shipsis only given to initialize the map internally. You must solve this problem "blindfolded". In other words, you must find the answer using the givenhasShipsAPI, without knowing theshipsposition. 0 <= bottomLeft[0] <= topRight[0] <= 10000 <= bottomLeft[1] <= topRight[1] <= 1000topRight != bottomLeft
Solutions
Solution 1: Recursion + Divide and Conquer
Since there are at most $10$ ships in the rectangle, we can divide the rectangle into four sub-rectangles, calculate the number of ships in each sub-rectangle, and then add the number of ships in the four sub-rectangles. If there are no ships in a sub-rectangle, then there is no need to continue dividing.
The time complexity is $O(C \times \log \max(m, n))$, and the space complexity is $O(\log \max(m, n))$. Where $C$ is the number of ships, and $m$ and $n$ are the length and width of the rectangle, respectively.
-
/** * // This is Sea's API interface. * // You should not implement it, or speculate about its implementation * class Sea { * public boolean hasShips(int[] topRight, int[] bottomLeft); * } */ class Solution { public int countShips(Sea sea, int[] topRight, int[] bottomLeft) { int x1 = bottomLeft[0], y1 = bottomLeft[1]; int x2 = topRight[0], y2 = topRight[1]; if (x1 > x2 || y1 > y2) { return 0; } if (!sea.hasShips(topRight, bottomLeft)) { return 0; } if (x1 == x2 && y1 == y2) { return 1; } int midx = (x1 + x2) >> 1; int midy = (y1 + y2) >> 1; int a = countShips(sea, topRight, new int[] {midx + 1, midy + 1}); int b = countShips(sea, new int[] {midx, y2}, new int[] {x1, midy + 1}); int c = countShips(sea, new int[] {midx, midy}, bottomLeft); int d = countShips(sea, new int[] {x2, midy}, new int[] {midx + 1, y1}); return a + b + c + d; } } -
/** * // This is Sea's API interface. * // You should not implement it, or speculate about its implementation * class Sea { * public: * bool hasShips(vector<int> topRight, vector<int> bottomLeft); * }; */ class Solution { public: int countShips(Sea sea, vector<int> topRight, vector<int> bottomLeft) { int x1 = bottomLeft[0], y1 = bottomLeft[1]; int x2 = topRight[0], y2 = topRight[1]; if (x1 > x2 || y1 > y2) { return 0; } if (!sea.hasShips(topRight, bottomLeft)) { return 0; } if (x1 == x2 && y1 == y2) { return 1; } int midx = (x1 + x2) >> 1; int midy = (y1 + y2) >> 1; int a = countShips(sea, topRight, {midx + 1, midy + 1}); int b = countShips(sea, {midx, y2}, {x1, midy + 1}); int c = countShips(sea, {midx, midy}, bottomLeft); int d = countShips(sea, {x2, midy}, {midx + 1, y1}); return a + b + c + d; } }; -
# """ # This is Sea's API interface. # You should not implement it, or speculate about its implementation # """ # class Sea: # def hasShips(self, topRight: 'Point', bottomLeft: 'Point') -> bool: # # class Point: # def __init__(self, x: int, y: int): # self.x = x # self.y = y class Solution: def countShips(self, sea: "Sea", topRight: "Point", bottomLeft: "Point") -> int: def dfs(topRight, bottomLeft): x1, y1 = bottomLeft.x, bottomLeft.y x2, y2 = topRight.x, topRight.y if x1 > x2 or y1 > y2: return 0 if not sea.hasShips(topRight, bottomLeft): return 0 if x1 == x2 and y1 == y2: return 1 midx = (x1 + x2) >> 1 midy = (y1 + y2) >> 1 a = dfs(topRight, Point(midx + 1, midy + 1)) b = dfs(Point(midx, y2), Point(x1, midy + 1)) c = dfs(Point(midx, midy), bottomLeft) d = dfs(Point(x2, midy), Point(midx + 1, y1)) return a + b + c + d return dfs(topRight, bottomLeft) -
/** * // This is Sea's API interface. * // You should not implement it, or speculate about its implementation * type Sea struct { * func hasShips(topRight, bottomLeft []int) bool {} * } */ func countShips(sea Sea, topRight, bottomLeft []int) int { x1, y1 := bottomLeft[0], bottomLeft[1] x2, y2 := topRight[0], topRight[1] if x1 > x2 || y1 > y2 { return 0 } if !sea.hasShips(topRight, bottomLeft) { return 0 } if x1 == x2 && y1 == y2 { return 1 } midx := (x1 + x2) >> 1 midy := (y1 + y2) >> 1 a := countShips(sea, topRight, []int{midx + 1, midy + 1}) b := countShips(sea, []int{midx, y2}, []int{x1, midy + 1}) c := countShips(sea, []int{midx, midy}, bottomLeft) d := countShips(sea, []int{x2, midy}, []int{midx + 1, y1}) return a + b + c + d } -
/** * // This is the Sea's API interface. * // You should not implement it, or speculate about its implementation * class Sea { * hasShips(topRight: number[], bottomLeft: number[]): boolean {} * } */ function countShips(sea: Sea, topRight: number[], bottomLeft: number[]): number { const [x1, y1] = bottomLeft; const [x2, y2] = topRight; if (x1 > x2 || y1 > y2 || !sea.hasShips(topRight, bottomLeft)) { return 0; } if (x1 === x2 && y1 === y2) { return 1; } const midx = (x1 + x2) >> 1; const midy = (y1 + y2) >> 1; const a = countShips(sea, topRight, [midx + 1, midy + 1]); const b = countShips(sea, [midx, y2], [x1, midy + 1]); const c = countShips(sea, [midx, midy], bottomLeft); const d = countShips(sea, [x2, midy], [midx + 1, y1]); return a + b + c + d; }