Welcome to Subscribe On Youtube
1273. Delete Tree Nodes
Description
A tree rooted at node 0 is given as follows:
- The number of nodes is
nodes; - The value of the
ithnode isvalue[i]; - The parent of the
ithnode isparent[i].
Remove every subtree whose sum of values of nodes is zero.
Return the number of the remaining nodes in the tree.
Example 1:
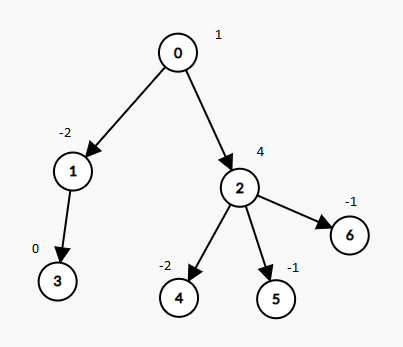
Input: nodes = 7, parent = [-1,0,0,1,2,2,2], value = [1,-2,4,0,-2,-1,-1] Output: 2
Example 2:
Input: nodes = 7, parent = [-1,0,0,1,2,2,2], value = [1,-2,4,0,-2,-1,-2] Output: 6
Constraints:
1 <= nodes <= 104parent.length == nodes0 <= parent[i] <= nodes - 1parent[0] == -1which indicates that0is the root.value.length == nodes-105 <= value[i] <= 105- The given input is guaranteed to represent a valid tree.
Solutions
Solution 1: DFS
First, we convert the tree into a graph $g$, where $g[i]$ represents all the child nodes of node $i$.
Then we design a function $dfs(i)$, which represents the number of nodes and the sum of the weights in the subtree rooted at node $i$. The answer is $dfs(0)[1]$.
In this function, we recursively calculate the number of nodes and the sum of the weights in the subtree rooted at each child node $j$, and then accumulate these values. If the accumulated value is zero, we set the number of nodes in this subtree to zero. Finally, we return the number of nodes and the sum of the weights in the subtree rooted at node $i$.
The time complexity is $O(n)$, and the space complexity is $O(n)$. Where $n$ is the number of nodes in the tree.
-
class Solution { private List<Integer>[] g; private int[] value; public int deleteTreeNodes(int nodes, int[] parent, int[] value) { g = new List[nodes]; Arrays.setAll(g, k -> new ArrayList<>()); for (int i = 1; i < nodes; ++i) { g[parent[i]].add(i); } this.value = value; return dfs(0)[1]; } private int[] dfs(int i) { int[] res = new int[] {value[i], 1}; for (int j : g[i]) { int[] t = dfs(j); res[0] += t[0]; res[1] += t[1]; } if (res[0] == 0) { res[1] = 0; } return res; } } -
class Solution { public: int deleteTreeNodes(int nodes, vector<int>& parent, vector<int>& value) { vector<vector<int>> g(nodes); for (int i = 1; i < nodes; ++i) { g[parent[i]].emplace_back(i); } function<pair<int, int>(int)> dfs = [&](int i) -> pair<int, int> { int s = value[i], m = 1; for (int j : g[i]) { auto [t, n] = dfs(j); s += t; m += n; } if (s == 0) { m = 0; } return pair<int, int>{s, m}; }; return dfs(0).second; } }; -
class Solution: def deleteTreeNodes(self, nodes: int, parent: List[int], value: List[int]) -> int: def dfs(i): s, m = value[i], 1 for j in g[i]: t, n = dfs(j) s += t m += n if s == 0: m = 0 return (s, m) g = defaultdict(list) for i in range(1, nodes): g[parent[i]].append(i) return dfs(0)[1] -
func deleteTreeNodes(nodes int, parent []int, value []int) int { g := make([][]int, nodes) for i := 1; i < nodes; i++ { g[parent[i]] = append(g[parent[i]], i) } type pair struct{ s, n int } var dfs func(int) pair dfs = func(i int) pair { s, m := value[i], 1 for _, j := range g[i] { t := dfs(j) s += t.s m += t.n } if s == 0 { m = 0 } return pair{s, m} } return dfs(0).n }