Welcome to Subscribe On Youtube

1256. Encode Number

Description

Given a non-negative integer num, Return its encoding string.

The encoding is done by converting the integer to a string using a secret function that you should deduce from the following table:

 

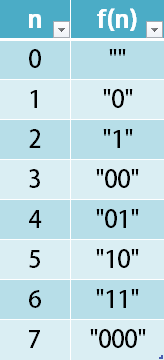
Example 1:

Input: num = 23
Output: "1000"

Example 2:

Input: num = 107
Output: "101100"

 

Constraints:

• 0 <= num <= 10^9

Solutions

Solution 1: Bit Manipulation

We add one to $num$, then convert it to a binary string and remove the highest bit $1$.

The time complexity is $O(\log n)$, and the space complexity is $O(\log n)$. Where $n$ is the size of $num$.

• Java
• C++
• Python
• Go
• TypeScript

• class Solution {
      public String encode(int num) {
          return Integer.toBinaryString(num + 1).substring(1);
      }
  }
  

• class Solution {
  public:
      string encode(int num) {
          bitset<32> bs(++num);
          string ans = bs.to_string();
          int i = 0;
          while (ans[i] == '0') {
              ++i;
          }
          return ans.substr(i + 1);
      }
  };
  

• class Solution:
      def encode(self, num: int) -> str:
          return bin(num + 1)[3:]
  
  

• func encode(num int) string {
  	num++
  	s := strconv.FormatInt(int64(num), 2)
  	return s[1:]
  }
  

• function encode(num: number): string {
      ++num;
      let s = num.toString(2);
      return s.slice(1);
  }
  
  

All Problems

All Solutions