Welcome to Subscribe On Youtube
1252. Cells with Odd Values in a Matrix
Description
There is an m x n matrix that is initialized to all 0's. There is also a 2D array indices where each indices[i] = [ri, ci] represents a 0-indexed location to perform some increment operations on the matrix.
For each location indices[i], do both of the following:
- Increment all the cells on row
ri. - Increment all the cells on column
ci.
Given m, n, and indices, return the number of odd-valued cells in the matrix after applying the increment to all locations in indices.
Example 1:
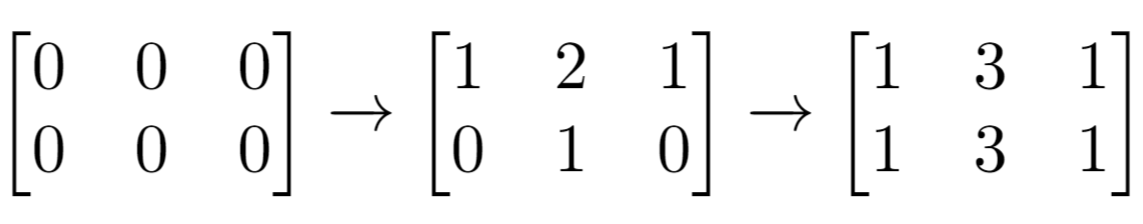
Input: m = 2, n = 3, indices = [[0,1],[1,1]] Output: 6 Explanation: Initial matrix = [[0,0,0],[0,0,0]]. After applying first increment it becomes [[1,2,1],[0,1,0]]. The final matrix is [[1,3,1],[1,3,1]], which contains 6 odd numbers.
Example 2:
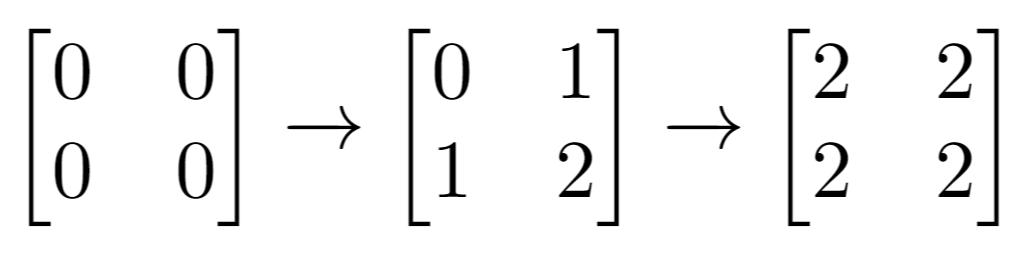
Input: m = 2, n = 2, indices = [[1,1],[0,0]] Output: 0 Explanation: Final matrix = [[2,2],[2,2]]. There are no odd numbers in the final matrix.
Constraints:
1 <= m, n <= 501 <= indices.length <= 1000 <= ri < m0 <= ci < n
Follow up: Could you solve this in O(n + m + indices.length) time with only O(n + m) extra space?
Solutions
Solution 1: Simulation
We create a matrix $g$ to store the results of the operations. For each pair $(r_i, c_i)$ in $indices$, we add $1$ to all elements in the $r_i$th row and the $c_i$th column of the matrix.
After the simulation, we traverse the matrix and count the number of odd numbers.
The time complexity is $O(\text{indices.length} \times (m+n) + mn)$, and the space complexity is $O(mn)$.
Solution 2: Space Optimization
We use row array $row$ and column array $col$ to record the number of times each row and column are increased. For each pair $(r_i, c_i)$ in $indices$, we add $1$ to $row[r_i]$ and $col[c_i]$ respectively.
After the operation, we can calculate that the count at position $(i, j)$ is $row[i] + col[j]$. We traverse the matrix and count the number of odd numbers.
The time complexity is $O(\text{indices.length} + mn)$, and the space complexity is $O(m+n)$.
Solution 3: Mathematical Optimization
We notice that only when exactly one of $row[i]$ and $col[j]$ is odd, the number at position $(i, j)$ in the matrix will be odd.
We count the number of odd numbers in $row$, denoted as $cnt1$; the number of odd numbers in $col$, denoted as $cnt2$. Then the final number of odd numbers is $cnt1 \times (n-cnt2) + cnt2 \times (m-cnt1)$.
The time complexity is $O(\text{indices.length} + m + n)$, and the space complexity is $O(m+n)$.
-
class Solution { public int oddCells(int m, int n, int[][] indices) { int[][] g = new int[m][n]; for (int[] e : indices) { int r = e[0], c = e[1]; for (int i = 0; i < m; ++i) { g[i][c]++; } for (int j = 0; j < n; ++j) { g[r][j]++; } } int ans = 0; for (int[] row : g) { for (int v : row) { ans += v % 2; } } return ans; } } -
class Solution { public: int oddCells(int m, int n, vector<vector<int>>& indices) { vector<vector<int>> g(m, vector<int>(n)); for (auto& e : indices) { int r = e[0], c = e[1]; for (int i = 0; i < m; ++i) ++g[i][c]; for (int j = 0; j < n; ++j) ++g[r][j]; } int ans = 0; for (auto& row : g) for (int v : row) ans += v % 2; return ans; } }; -
class Solution: def oddCells(self, m: int, n: int, indices: List[List[int]]) -> int: g = [[0] * n for _ in range(m)] for r, c in indices: for i in range(m): g[i][c] += 1 for j in range(n): g[r][j] += 1 return sum(v % 2 for row in g for v in row) -
func oddCells(m int, n int, indices [][]int) int { g := make([][]int, m) for i := range g { g[i] = make([]int, n) } for _, e := range indices { r, c := e[0], e[1] for i := 0; i < m; i++ { g[i][c]++ } for j := 0; j < n; j++ { g[r][j]++ } } ans := 0 for _, row := range g { for _, v := range row { ans += v % 2 } } return ans }