1235. Maximum Profit in Job Scheduling

Description

We have n jobs, where every job is scheduled to be done from startTime[i] to endTime[i], obtaining a profit of profit[i].

You're given the startTime, endTime and profit arrays, return the maximum profit you can take such that there are no two jobs in the subset with overlapping time range.

If you choose a job that ends at time X you will be able to start another job that starts at time X.

Example 1:

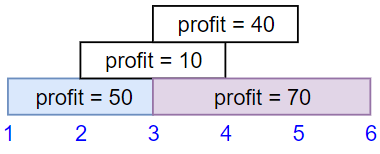
Input: startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
Output: 120
Explanation: The subset chosen is the first and fourth job. 
Time range [1-3]+[3-6] , we get profit of 120 = 50 + 70.

Example 2:

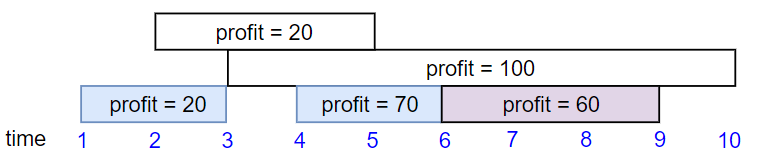
Input: startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
Output: 150
Explanation: The subset chosen is the first, fourth and fifth job. 
Profit obtained 150 = 20 + 70 + 60.

Example 3:

Input: startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
Output: 6

Constraints:

1 <= startTime.length == endTime.length == profit.length <= 5 * 10⁴
1 <= startTime[i] < endTime[i] <= 10⁹
1 <= profit[i] <= 10⁴

Solutions

Solution 1: Memoization Search + Binary Search

First, we sort the jobs by start time in ascending order, then design a function $dfs(i)$ to represent the maximum profit that can be obtained starting from the $i$-th job. The answer is $dfs(0)$.

The calculation process of function $dfs(i)$ is as follows:

For the $i$-th job, we can choose to do it or not. If we don’t do it, the maximum profit is $dfs(i + 1)$; if we do it, we can use binary search to find the first job that starts after the end time of the $i$-th job, denoted as $j$, then the maximum profit is $profit[i] + dfs(j)$. We take the larger of the two. That is:

\[dfs(i)=\max(dfs(i+1),profit[i]+dfs(j))\]

Where $j$ is the smallest index that satisfies $startTime[j] \ge endTime[i]$.

In this process, we can use memoization search to save the answer of each state to avoid repeated calculations.

The time complexity is $O(n \times \log n)$, where $n$ is the number of jobs.

Solution 2: Dynamic Programming + Binary Search

We can also change the memoization search in Solution 1 to dynamic programming.

First, sort the jobs, this time we sort by end time in ascending order, then define $dp[i]$, which represents the maximum profit that can be obtained from the first $i$ jobs. The answer is $dp[n]$. Initialize $dp[0]=0$.

For the $i$-th job, we can choose to do it or not. If we don’t do it, the maximum profit is $dp[i]$; if we do it, we can use binary search to find the last job that ends before the start time of the $i$-th job, denoted as $j$, then the maximum profit is $profit[i] + dp[j]$. We take the larger of the two. That is:

\[dp[i+1] = \max(dp[i], profit[i] + dp[j])\]

Where $j$ is the largest index that satisfies $endTime[j] \leq startTime[i]$.

The time complexity is $O(n \times \log n)$, where $n$ is the number of jobs.

class Solution {
    private int[][] jobs;
    private int[] f;
    private int n;

    public int jobScheduling(int[] startTime, int[] endTime, int[] profit) {
        n = profit.length;
        jobs = new int[n][3];
        for (int i = 0; i < n; ++i) {
            jobs[i] = new int[] {startTime[i], endTime[i], profit[i]};
        }
        Arrays.sort(jobs, (a, b) -> a[0] - b[0]);
        f = new int[n];
        return dfs(0);
    }

    private int dfs(int i) {
        if (i >= n) {
            return 0;
        }
        if (f[i] != 0) {
            return f[i];
        }
        int e = jobs[i][1], p = jobs[i][2];
        int j = search(jobs, e, i + 1);
        int ans = Math.max(dfs(i + 1), p + dfs(j));
        f[i] = ans;
        return ans;
    }

    private int search(int[][] jobs, int x, int i) {
        int left = i, right = n;
        while (left < right) {
            int mid = (left + right) >> 1;
            if (jobs[mid][0] >= x) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return left;
    }
}

class Solution {
public:
    int jobScheduling(vector<int>& startTime, vector<int>& endTime, vector<int>& profit) {
        int n = profit.size();
        vector<tuple<int, int, int>> jobs(n);
        for (int i = 0; i < n; ++i) jobs[i] = {startTime[i], endTime[i], profit[i]};
        sort(jobs.begin(), jobs.end());
        vector<int> f(n);
        function<int(int)> dfs = [&](int i) -> int {
            if (i >= n) return 0;
            if (f[i]) return f[i];
            auto [_, e, p] = jobs[i];
            tuple<int, int, int> t{e, 0, 0};
            int j = lower_bound(jobs.begin() + i + 1, jobs.end(), t, [&](auto& l, auto& r) -> bool { return get<0>(l) < get<0>(r); }) - jobs.begin();
            int ans = max(dfs(i + 1), p + dfs(j));
            f[i] = ans;
            return ans;
        };
        return dfs(0);
    }
};

class Solution:
    def jobScheduling(
        self, startTime: List[int], endTime: List[int], profit: List[int]
    ) -> int:
        @cache
        def dfs(i):
            if i >= n:
                return 0
            _, e, p = jobs[i]
            j = bisect_left(jobs, e, lo=i + 1, key=lambda x: x[0])
            return max(dfs(i + 1), p + dfs(j))

        jobs = sorted(zip(startTime, endTime, profit))
        n = len(profit)
        return dfs(0)

func jobScheduling(startTime []int, endTime []int, profit []int) int {
	n := len(profit)
	type tuple struct{ s, e, p int }
	jobs := make([]tuple, n)
	for i, p := range profit {
		jobs[i] = tuple{startTime[i], endTime[i], p}
	}
	sort.Slice(jobs, func(i, j int) bool { return jobs[i].s < jobs[j].s })
	f := make([]int, n)
	var dfs func(int) int
	dfs = func(i int) int {
		if i >= n {
			return 0
		}
		if f[i] != 0 {
			return f[i]
		}
		j := sort.Search(n, func(j int) bool { return jobs[j].s >= jobs[i].e })
		ans := max(dfs(i+1), jobs[i].p+dfs(j))
		f[i] = ans
		return ans
	}
	return dfs(0)
}

function jobScheduling(startTime: number[], endTime: number[], profit: number[]): number {
    const n = startTime.length;
    const f = new Array(n).fill(0);
    const idx = new Array(n).fill(0).map((_, i) => i);
    idx.sort((i, j) => startTime[i] - startTime[j]);
    const search = (x: number) => {
        let l = 0;
        let r = n;
        while (l < r) {
            const mid = (l + r) >> 1;
            if (startTime[idx[mid]] >= x) {
                r = mid;
            } else {
                l = mid + 1;
            }
        }
        return l;
    };
    const dfs = (i: number): number => {
        if (i >= n) {
            return 0;
        }
        if (f[i] !== 0) {
            return f[i];
        }
        const j = search(endTime[idx[i]]);
        return (f[i] = Math.max(dfs(i + 1), dfs(j) + profit[idx[i]]));
    };
    return dfs(0);
}

class Solution {

    func binarySearch<T: Comparable>(inputArr: [T], searchItem: T) -> Int? {
        var lowerIndex = 0
        var upperIndex = inputArr.count - 1

        while lowerIndex < upperIndex {
            let currentIndex = (lowerIndex + upperIndex) / 2
            if inputArr[currentIndex] <= searchItem {
                lowerIndex = currentIndex + 1
            } else {
                upperIndex = currentIndex
            }
        }

        if inputArr[upperIndex] <= searchItem {
            return upperIndex + 1
        }
        return lowerIndex
    }

    func jobScheduling(_ startTime: [Int], _ endTime: [Int], _ profit: [Int]) -> Int {
        let zipList = zip(zip(startTime, endTime), profit)
        var table: [(startTime: Int, endTime: Int, profit: Int, cumsum: Int)] = []

        for ((x, y), z) in zipList {
            table.append((x, y, z, 0))
        }
        table.sort(by: { $0.endTime < $1.endTime })
        let sortedEndTime = endTime.sorted()

        var profits: [Int] = [0]
        for iJob in table {
            let index: Int! = binarySearch(inputArr: sortedEndTime, searchItem: iJob.startTime)
            if profits.last! < profits[index] + iJob.profit {
                profits.append(profits[index] + iJob.profit)
            } else {
                profits.append(profits.last!)
            }
        }
        return profits.last!
    }
}

1235 - Maximum Profit in Job Scheduling

1235. Maximum Profit in Job Scheduling

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

1235. Maximum Profit in Job Scheduling

Description

Solutions

All Problems

All Solutions