Welcome to Subscribe On Youtube
1222. Queens That Can Attack the King
Description
On a 0-indexed 8 x 8 chessboard, there can be multiple black queens and one white king.
You are given a 2D integer array queens where queens[i] = [xQueeni, yQueeni] represents the position of the ith black queen on the chessboard. You are also given an integer array king of length 2 where king = [xKing, yKing] represents the position of the white king.
Return the coordinates of the black queens that can directly attack the king. You may return the answer in any order.
Example 1:
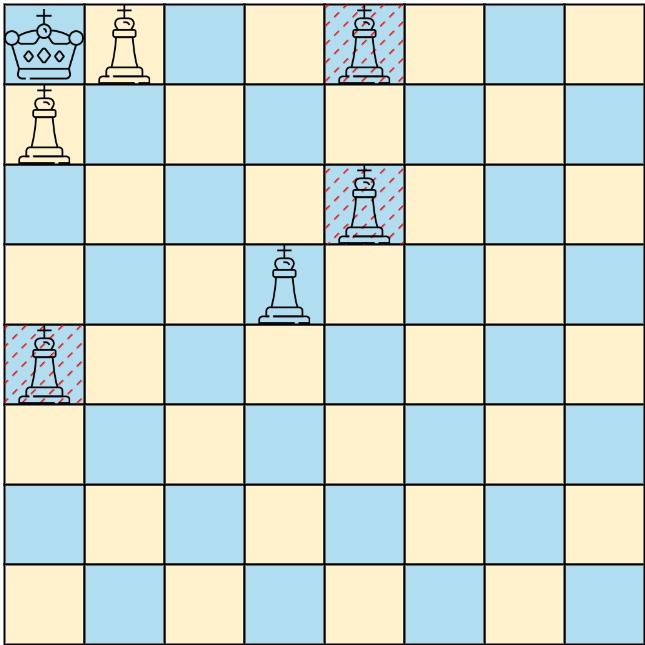
Input: queens = [[0,1],[1,0],[4,0],[0,4],[3,3],[2,4]], king = [0,0] Output: [[0,1],[1,0],[3,3]] Explanation: The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
Example 2:
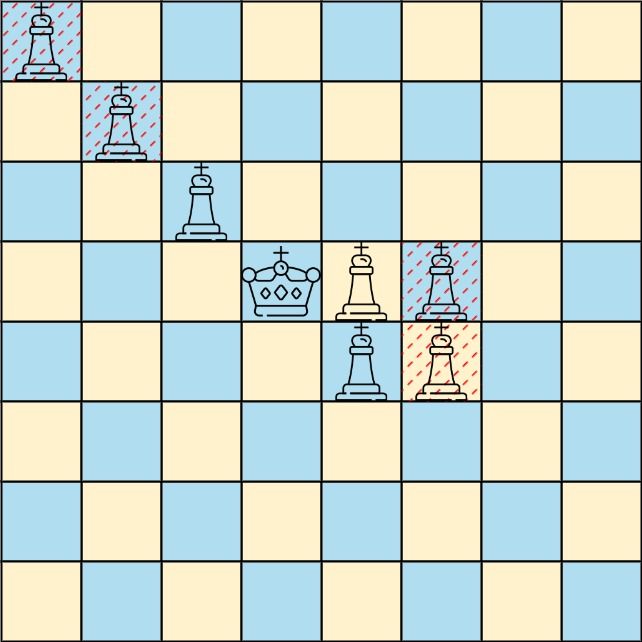
Input: queens = [[0,0],[1,1],[2,2],[3,4],[3,5],[4,4],[4,5]], king = [3,3] Output: [[2,2],[3,4],[4,4]] Explanation: The diagram above shows the three queens that can directly attack the king and the three queens that cannot attack the king (i.e., marked with red dashes).
Constraints:
1 <= queens.length < 64queens[i].length == king.length == 20 <= xQueeni, yQueeni, xKing, yKing < 8- All the given positions are unique.
Solutions
Solution 1: Direct Search
First, we store all the positions of the queens in a hash table or a two-dimensional array $s$.
Next, starting from the position of the king, we search in the eight directions: up, down, left, right, upper left, upper right, lower left, and lower right. If there is a queen in a certain direction, we add its position to the answer and stop continuing to search in that direction.
After the search is over, we return the answer.
The time complexity is $O(n^2)$, and the space complexity is $O(n^2)$. In this problem, $n = 8$.
-
class Solution { public List<List<Integer>> queensAttacktheKing(int[][] queens, int[] king) { final int n = 8; var s = new boolean[n][n]; for (var q : queens) { s[q[0]][q[1]] = true; } List<List<Integer>> ans = new ArrayList<>(); for (int a = -1; a <= 1; ++a) { for (int b = -1; b <= 1; ++b) { if (a != 0 || b != 0) { int x = king[0] + a, y = king[1] + b; while (x >= 0 && x < n && y >= 0 && y < n) { if (s[x][y]) { ans.add(List.of(x, y)); break; } x += a; y += b; } } } } return ans; } } -
class Solution { public: vector<vector<int>> queensAttacktheKing(vector<vector<int>>& queens, vector<int>& king) { int n = 8; bool s[8][8]{}; for (auto& q : queens) { s[q[0]][q[1]] = true; } vector<vector<int>> ans; for (int a = -1; a <= 1; ++a) { for (int b = -1; b <= 1; ++b) { if (a || b) { int x = king[0] + a, y = king[1] + b; while (x >= 0 && x < n && y >= 0 && y < n) { if (s[x][y]) { ans.push_back({x, y}); break; } x += a; y += b; } } } } return ans; } }; -
class Solution: def queensAttacktheKing( self, queens: List[List[int]], king: List[int] ) -> List[List[int]]: n = 8 s = {(i, j) for i, j in queens} ans = [] for a in range(-1, 2): for b in range(-1, 2): if a or b: x, y = king while 0 <= x + a < n and 0 <= y + b < n: x, y = x + a, y + b if (x, y) in s: ans.append([x, y]) break return ans -
func queensAttacktheKing(queens [][]int, king []int) (ans [][]int) { n := 8 s := [8][8]bool{} for _, q := range queens { s[q[0]][q[1]] = true } for a := -1; a <= 1; a++ { for b := -1; b <= 1; b++ { if a != 0 || b != 0 { x, y := king[0]+a, king[1]+b for 0 <= x && x < n && 0 <= y && y < n { if s[x][y] { ans = append(ans, []int{x, y}) break } x += a y += b } } } } return } -
function queensAttacktheKing(queens: number[][], king: number[]): number[][] { const n = 8; const s: boolean[][] = Array.from({ length: n }, () => Array.from({ length: n }, () => false)); queens.forEach(([x, y]) => (s[x][y] = true)); const ans: number[][] = []; for (let a = -1; a <= 1; ++a) { for (let b = -1; b <= 1; ++b) { if (a || b) { let [x, y] = [king[0] + a, king[1] + b]; while (x >= 0 && x < n && y >= 0 && y < n) { if (s[x][y]) { ans.push([x, y]); break; } x += a; y += b; } } } } return ans; }