Welcome to Subscribe On Youtube
1184. Distance Between Bus Stops
Description
A bus has n stops numbered from 0 to n - 1 that form a circle. We know the distance between all pairs of neighboring stops where distance[i] is the distance between the stops number i and (i + 1) % n.
The bus goes along both directions i.e. clockwise and counterclockwise.
Return the shortest distance between the given start and destination stops.
Example 1:
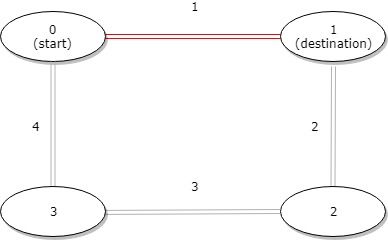
Input: distance = [1,2,3,4], start = 0, destination = 1 Output: 1 Explanation: Distance between 0 and 1 is 1 or 9, minimum is 1.
Example 2:
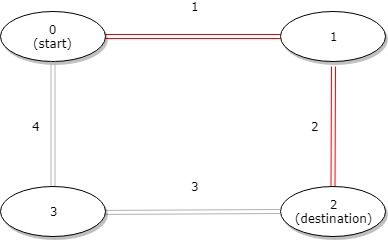
Input: distance = [1,2,3,4], start = 0, destination = 2 Output: 3 Explanation: Distance between 0 and 2 is 3 or 7, minimum is 3.
Example 3:
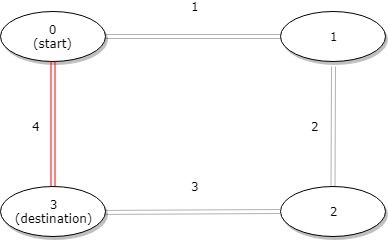
Input: distance = [1,2,3,4], start = 0, destination = 3 Output: 4 Explanation: Distance between 0 and 3 is 6 or 4, minimum is 4.
Constraints:
1 <= n <= 10^4distance.length == n0 <= start, destination < n0 <= distance[i] <= 10^4
Solutions
Solution 1: Simulation
First, we can calculate the total distance $s$ that the bus travels. Then, we simulate the bus’s journey, starting from the departure point, moving one stop to the right each time, until we reach the destination. During the simulation, we can record the distance $a$ from the departure point to the destination. Therefore, the shortest distance from the destination to the departure point is $\min(a, s - a)$.
The time complexity is $O(n)$, where $n$ is the number of bus stops. The space complexity is $O(1)$.
-
class Solution { public int distanceBetweenBusStops(int[] distance, int start, int destination) { int s = Arrays.stream(distance).sum(); int n = distance.length; int a = 0; while (start != destination) { a += distance[start]; start = (start + 1) % n; } return Math.min(a, s - a); } } -
class Solution { public: int distanceBetweenBusStops(vector<int>& distance, int start, int destination) { int s = accumulate(distance.begin(), distance.end(), 0); int a = 0, n = distance.size(); while (start != destination) { a += distance[start]; start = (start + 1) % n; } return min(a, s - a); } }; -
class Solution: def distanceBetweenBusStops( self, distance: List[int], start: int, destination: int ) -> int: a, n = 0, len(distance) while start != destination: a += distance[start] start = (start + 1) % n return min(a, sum(distance) - a) -
func distanceBetweenBusStops(distance []int, start int, destination int) int { s := 0 for _, x := range distance { s += x } a, n := 0, len(distance) for start != destination { a += distance[start] start = (start + 1) % n } return min(a, s-a) } -
function distanceBetweenBusStops(distance: number[], start: number, destination: number): number { const s = distance.reduce((a, b) => a + b, 0); let a = 0; const n = distance.length; while (start != destination) { a += distance[start]; start = (start + 1) % n; } return Math.min(a, s - a); } -
/** * @param {number[]} distance * @param {number} start * @param {number} destination * @return {number} */ var distanceBetweenBusStops = function (distance, start, destination) { const s = distance.reduce((a, b) => a + b, 0); let a = 0; const n = distance.length; while (start != destination) { a += distance[start]; start = (start + 1) % n; } return Math.min(a, s - a); }; -
impl Solution { pub fn distance_between_bus_stops(distance: Vec<i32>, start: i32, destination: i32) -> i32 { let s: i32 = distance.iter().sum(); let mut t = 0; let n = distance.len(); let mut start = start as usize; let destination = destination as usize; while start != destination { t += distance[start]; start = (start + 1) % n; } t.min(s - t) } }