Welcome to Subscribe On Youtube

1028. Recover a Tree From Preorder Traversal

Description

We run a preorder depth-first search (DFS) on the root of a binary tree.

At each node in this traversal, we output D dashes (where D is the depth of this node), then we output the value of this node.  If the depth of a node is D, the depth of its immediate child is D + 1.  The depth of the root node is 0.

If a node has only one child, that child is guaranteed to be the left child.

Given the output traversal of this traversal, recover the tree and return its root.

 

Example 1:

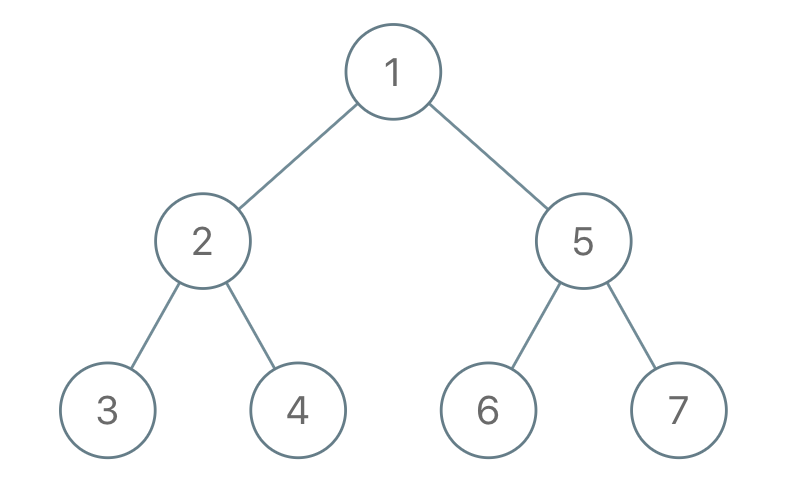
Input: traversal = "1-2--3--4-5--6--7"
Output: [1,2,5,3,4,6,7]

Example 2:

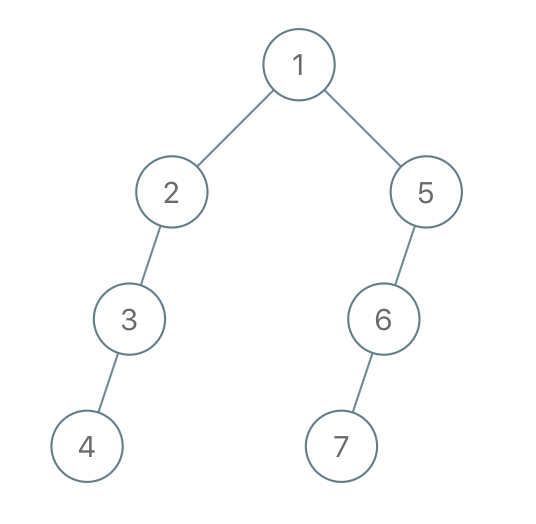
Input: traversal = "1-2--3---4-5--6---7"
Output: [1,2,5,3,null,6,null,4,null,7]

Example 3:

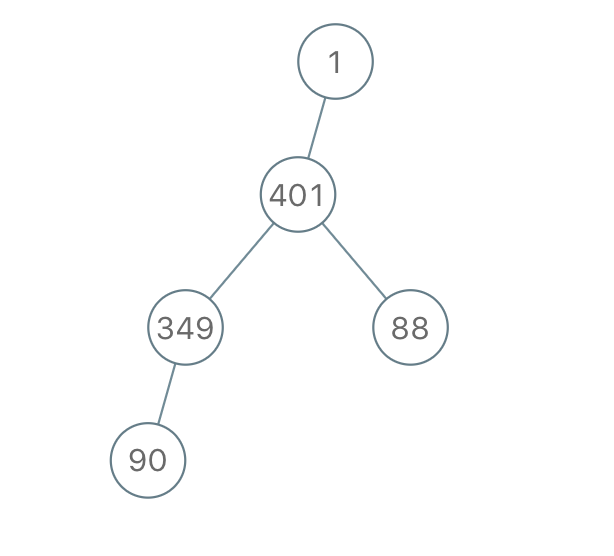
Input: traversal = "1-401--349---90--88"
Output: [1,401,null,349,88,90]

 

Constraints:

  • The number of nodes in the original tree is in the range [1, 1000].
  • 1 <= Node.val <= 109

Solutions

  • /**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* recoverFromPreorder(string S) {
        stack<TreeNode*> st;
        int depth = 0;
        int num = 0;
        for (int i = 0; i < S.length(); ++i) {
            if (S[i] == '-') {
                depth++;
            } else {
                num = 10 * num + S[i] - '0';
            }
            if (i + 1 >= S.length() || (isdigit(S[i]) && S[i + 1] == '-')) {
                TreeNode* newNode = new TreeNode(num);
                while (st.size() > depth) {
                    st.pop();
                }
                if (!st.empty()) {
                    if (st.top()->left == nullptr) {
                        st.top()->left = newNode;
                    } else {
                        st.top()->right = newNode;
                    }
                }
                st.push(newNode);
                depth = 0;
                num = 0;
            }
        }
        TreeNode* res;
        while (!st.empty()) {
            res = st.top();
            st.pop();
        }
        return res;
    }
};

All Problems

All Solutions