Welcome to Subscribe On Youtube
987. Vertical Order Traversal of a Binary Tree
Description
Given the root of a binary tree, calculate the vertical order traversal of the binary tree.
For each node at position (row, col), its left and right children will be at positions (row + 1, col - 1) and (row + 1, col + 1) respectively. The root of the tree is at (0, 0).
The vertical order traversal of a binary tree is a list of top-to-bottom orderings for each column index starting from the leftmost column and ending on the rightmost column. There may be multiple nodes in the same row and same column. In such a case, sort these nodes by their values.
Return the vertical order traversal of the binary tree.
Example 1:
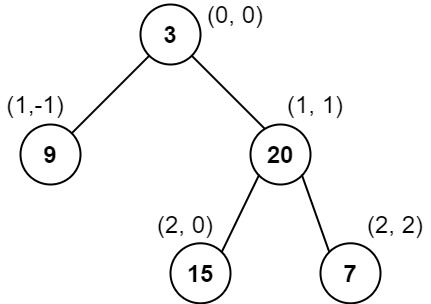
Input: root = [3,9,20,null,null,15,7] Output: [[9],[3,15],[20],[7]] Explanation: Column -1: Only node 9 is in this column. Column 0: Nodes 3 and 15 are in this column in that order from top to bottom. Column 1: Only node 20 is in this column. Column 2: Only node 7 is in this column.
Example 2:
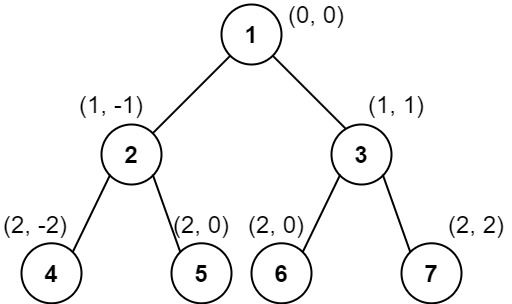
Input: root = [1,2,3,4,5,6,7]
Output: [[4],[2],[1,5,6],[3],[7]]
Explanation:
Column -2: Only node 4 is in this column.
Column -1: Only node 2 is in this column.
Column 0: Nodes 1, 5, and 6 are in this column.
1 is at the top, so it comes first.
5 and 6 are at the same position (2, 0), so we order them by their value, 5 before 6.
Column 1: Only node 3 is in this column.
Column 2: Only node 7 is in this column.
Example 3:
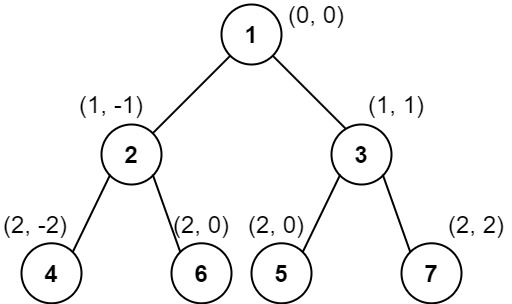
Input: root = [1,2,3,4,6,5,7] Output: [[4],[2],[1,5,6],[3],[7]] Explanation: This case is the exact same as example 2, but with nodes 5 and 6 swapped. Note that the solution remains the same since 5 and 6 are in the same location and should be ordered by their values.
Constraints:
- The number of nodes in the tree is in the range
[1, 1000]. 0 <= Node.val <= 1000
Solutions
-
class Solution { public List<List<Integer>> verticalTraversal(TreeNode root) { List<int[]> list = new ArrayList<>(); dfs(root, 0, 0, list); list.sort(new Comparator<int[]>() { @Override public int compare(int[] o1, int[] o2) { if (o1[0] != o2[0]) return Integer.compare(o1[0], o2[0]); if (o1[1] != o2[1]) return Integer.compare(o2[1], o1[1]); return Integer.compare(o1[2], o2[2]); } }); List<List<Integer>> res = new ArrayList<>(); int preX = 1; for (int[] cur : list) { if (preX != cur[0]) { res.add(new ArrayList<>()); preX = cur[0]; } res.get(res.size() - 1).add(cur[2]); } return res; } private void dfs(TreeNode root, int x, int y, List<int[]> list) { if (root == null) { return; } list.add(new int[] {x, y, root.val}); dfs(root.left, x - 1, y - 1, list); dfs(root.right, x + 1, y - 1, list); } } -
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def verticalTraversal(self, root: TreeNode) -> List[List[int]]: def dfs(root, i, j): if root is None: return nodes.append((i, j, root.val)) dfs(root.left, i + 1, j - 1) dfs(root.right, i + 1, j + 1) nodes = [] dfs(root, 0, 0) nodes.sort(key=lambda x: (x[1], x[0], x[2])) ans = [] prev = -2000 for i, j, v in nodes: if prev != j: ans.append([]) prev = j ans[-1].append(v) return ans -
/** * Definition for a binary tree node. * class TreeNode { * val: number * left: TreeNode | null * right: TreeNode | null * constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } * } */ function verticalTraversal(root: TreeNode | null): number[][] { let solution = []; dfs(root, 0, 0, solution); solution.sort(compare); let ans = []; let pre = Number.MIN_SAFE_INTEGER; for (let node of solution) { const [val, , idx] = node; if (idx != pre) { ans.push([]); pre = idx; } ans[ans.length - 1].push(val); } return ans; } function compare(a: Array<number>, b: Array<number>) { const [a0, a1, a2] = a, [b0, b1, b2] = b; if (a2 == b2) { if (a1 == b1) { return a0 - b0; } return a1 - b1; } return a2 - b2; } function dfs(root: TreeNode | null, depth: number, idx: number, solution: Array<Array<number>>) { if (!root) return; solution.push([root.val, depth, idx]); dfs(root.left, depth + 1, idx - 1, solution); dfs(root.right, depth + 1, idx + 1, solution); } -
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: vector<vector<int>> verticalTraversal(TreeNode* root) { vector<tuple<int, int, int>> nodes; function<void(TreeNode*, int, int)> dfs = [&](TreeNode* root, int i, int j) { if (!root) { return; } nodes.emplace_back(j, i, root->val); dfs(root->left, i + 1, j - 1); dfs(root->right, i + 1, j + 1); }; dfs(root, 0, 0); sort(nodes.begin(), nodes.end()); vector<vector<int>> ans; int prev = -2000; for (auto [j, _, val] : nodes) { if (j != prev) { prev = j; ans.emplace_back(); } ans.back().push_back(val); } return ans; } }; -
/** * Definition for a binary tree node. * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */ func verticalTraversal(root *TreeNode) (ans [][]int) { nodes := [][3]int{} var dfs func(*TreeNode, int, int) dfs = func(root *TreeNode, i, j int) { if root == nil { return } nodes = append(nodes, [3]int{j, i, root.Val}) dfs(root.Left, i+1, j-1) dfs(root.Right, i+1, j+1) } dfs(root, 0, 0) sort.Slice(nodes, func(i, j int) bool { a, b := nodes[i], nodes[j] return a[0] < b[0] || a[0] == b[0] && (a[1] < b[1] || a[1] == b[1] && a[2] < b[2]) }) prev := -2000 for _, node := range nodes { j, val := node[0], node[2] if j != prev { ans = append(ans, nil) prev = j } ans[len(ans)-1] = append(ans[len(ans)-1], val) } return }