Welcome to Subscribe On Youtube

986. Interval List Intersections

Description

You are given two lists of closed intervals, firstList and secondList, where firstList[i] = [starti, endi] and secondList[j] = [startj, endj]. Each list of intervals is pairwise disjoint and in sorted order.

Return the intersection of these two interval lists.

A closed interval [a, b] (with a <= b) denotes the set of real numbers x with a <= x <= b.

The intersection of two closed intervals is a set of real numbers that are either empty or represented as a closed interval. For example, the intersection of [1, 3] and [2, 4] is [2, 3].

 

Example 1:

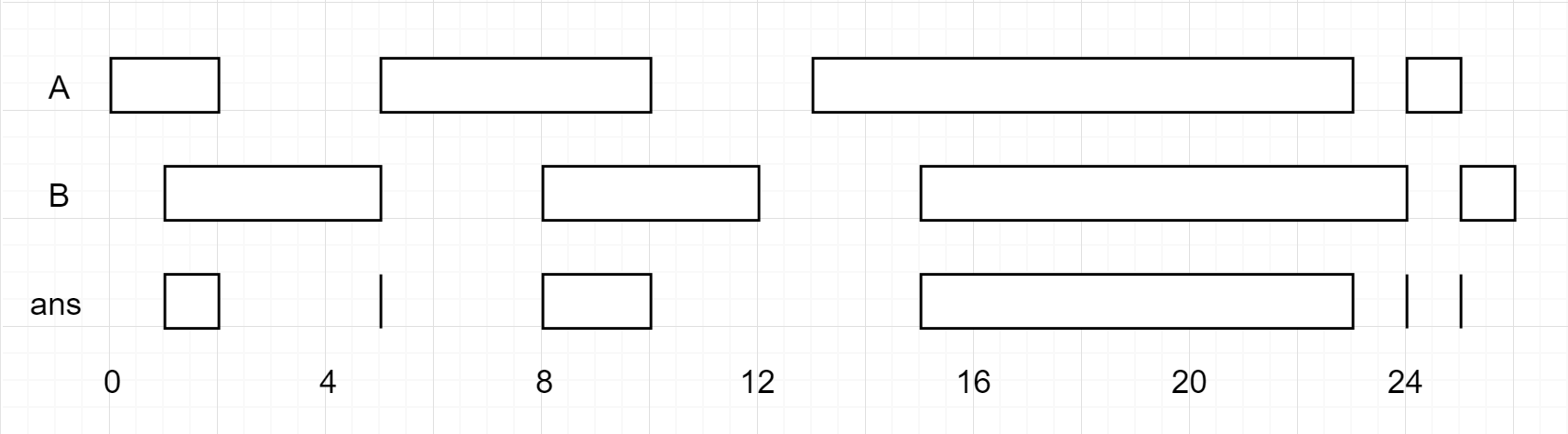
Input: firstList = [[0,2],[5,10],[13,23],[24,25]], secondList = [[1,5],[8,12],[15,24],[25,26]]
Output: [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]

Example 2:

Input: firstList = [[1,3],[5,9]], secondList = []
Output: []

 

Constraints:

• 0 <= firstList.length, secondList.length <= 1000
• firstList.length + secondList.length >= 1
• 0 <= starti < endi <= 109
• endi < starti+1
• 0 <= startj < endj <= 109
• endj < startj+1

Solutions

• Java
• C++
• Python
• Go
• TypeScript
• RenderScript

• class Solution {
      public int[][] intervalIntersection(int[][] firstList, int[][] secondList) {
          List<int[]> ans = new ArrayList<>();
          int m = firstList.length, n = secondList.length;
          for (int i = 0, j = 0; i < m && j < n;) {
              int l = Math.max(firstList[i][0], secondList[j][0]);
              int r = Math.min(firstList[i][1], secondList[j][1]);
              if (l <= r) {
                  ans.add(new int[] {l, r});
              }
              if (firstList[i][1] < secondList[j][1]) {
                  ++i;
              } else {
                  ++j;
              }
          }
          return ans.toArray(new int[ans.size()][]);
      }
  }
  

• class Solution {
  public:
      vector<vector<int>> intervalIntersection(vector<vector<int>>& firstList, vector<vector<int>>& secondList) {
          vector<vector<int>> ans;
          int m = firstList.size(), n = secondList.size();
          for (int i = 0, j = 0; i < m && j < n;) {
              int l = max(firstList[i][0], secondList[j][0]);
              int r = min(firstList[i][1], secondList[j][1]);
              if (l <= r) ans.push_back({l, r});
              if (firstList[i][1] < secondList[j][1])
                  ++i;
              else
                  ++j;
          }
          return ans;
      }
  };
  

• class Solution:
      def intervalIntersection(
          self, firstList: List[List[int]], secondList: List[List[int]]
      ) -> List[List[int]]:
          i = j = 0
          ans = []
          while i < len(firstList) and j < len(secondList):
              s1, e1, s2, e2 = *firstList[i], *secondList[j]
              l, r = max(s1, s2), min(e1, e2)
              if l <= r:
                  ans.append([l, r])
              if e1 < e2:
                  i += 1
              else:
                  j += 1
          return ans
  
  

• func intervalIntersection(firstList [][]int, secondList [][]int) [][]int {
  	m, n := len(firstList), len(secondList)
  	var ans [][]int
  	for i, j := 0, 0; i < m && j < n; {
  		l := max(firstList[i][0], secondList[j][0])
  		r := min(firstList[i][1], secondList[j][1])
  		if l <= r {
  			ans = append(ans, []int{l, r})
  		}
  		if firstList[i][1] < secondList[j][1] {
  			i++
  		} else {
  			j++
  		}
  	}
  	return ans
  }
  

• function intervalIntersection(firstList: number[][], secondList: number[][]): number[][] {
      const n = firstList.length;
      const m = secondList.length;
      const res = [];
      let i = 0;
      let j = 0;
      while (i < n && j < m) {
          const start = Math.max(firstList[i][0], secondList[j][0]);
          const end = Math.min(firstList[i][1], secondList[j][1]);
          if (start <= end) {
              res.push([start, end]);
          }
          if (firstList[i][1] < secondList[j][1]) {
              i++;
          } else {
              j++;
          }
      }
      return res;
  }
  
  

• impl Solution {
      pub fn interval_intersection(
          first_list: Vec<Vec<i32>>,
          second_list: Vec<Vec<i32>>
      ) -> Vec<Vec<i32>> {
          let n = first_list.len();
          let m = second_list.len();
          let mut res = Vec::new();
          let (mut i, mut j) = (0, 0);
          while i < n && j < m {
              let start = first_list[i][0].max(second_list[j][0]);
              let end = first_list[i][1].min(second_list[j][1]);
              if start <= end {
                  res.push(vec![start, end]);
              }
              if first_list[i][1] < second_list[j][1] {
                  i += 1;
              } else {
                  j += 1;
              }
          }
          res
      }
  }
  
  

All Problems

All Solutions