Welcome to Subscribe On Youtube
980. Unique Paths III
Description
You are given an m x n integer array grid where grid[i][j] could be:
1representing the starting square. There is exactly one starting square.2representing the ending square. There is exactly one ending square.0representing empty squares we can walk over.-1representing obstacles that we cannot walk over.
Return the number of 4-directional walks from the starting square to the ending square, that walk over every non-obstacle square exactly once.
Example 1:
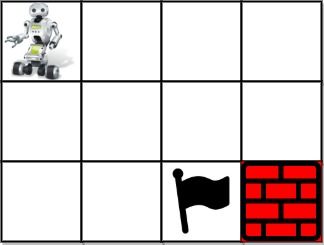
Input: grid = [[1,0,0,0],[0,0,0,0],[0,0,2,-1]] Output: 2 Explanation: We have the following two paths: 1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2) 2. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2)
Example 2:
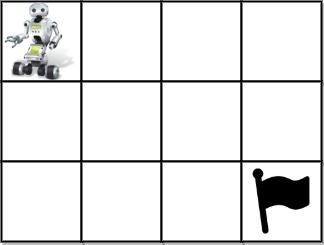
Input: grid = [[1,0,0,0],[0,0,0,0],[0,0,0,2]] Output: 4 Explanation: We have the following four paths: 1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2),(2,3) 2. (0,0),(0,1),(1,1),(1,0),(2,0),(2,1),(2,2),(1,2),(0,2),(0,3),(1,3),(2,3) 3. (0,0),(1,0),(2,0),(2,1),(2,2),(1,2),(1,1),(0,1),(0,2),(0,3),(1,3),(2,3) 4. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2),(2,3)
Example 3:

Input: grid = [[0,1],[2,0]] Output: 0 Explanation: There is no path that walks over every empty square exactly once. Note that the starting and ending square can be anywhere in the grid.
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 201 <= m * n <= 20-1 <= grid[i][j] <= 2- There is exactly one starting cell and one ending cell.
Solutions
Solution 1: Backtracking
We can first traverse the entire grid, find the starting point $(x, y)$, and count the number of blank spaces $cnt$.
Next, we can start searching from the starting point to get all the path numbers. We design a function $dfs(i, j, k)$ to indicate that the path number is $k$ and the starting point is $(i, j)$.
In the function, we first determine whether the current cell is the end point. If it is, we determine whether $k$ is equal to $cnt + 1$. If it is, the current path is a valid path, and $1$ is returned, otherwise $0$ is returned.
If the current cell is not the end point, we enumerate the four adjacent cells of the current cell. If the adjacent cell has not been visited, we mark the adjacent cell as visited, and then continue to search the path number from the adjacent cell. After the search is completed, we mark the adjacent cell as unvisited. After the search is completed, we return the sum of the path numbers of all adjacent cells.
Finally, we return the path number from the starting point, that is, $dfs(x, y, 1)$.
The time complexity is $O(3^{m \times n})$, and the space complexity is $O(m \times n)$. Where $m$ and $n$ are the number of rows and columns of the grid, respectively.
-
class Solution { private int m; private int n; private int cnt; private int[][] grid; private boolean[][] vis; public int uniquePathsIII(int[][] grid) { m = grid.length; n = grid[0].length; this.grid = grid; int x = 0, y = 0; for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { if (grid[i][j] == 0) { ++cnt; } else if (grid[i][j] == 1) { x = i; y = j; } } } vis = new boolean[m][n]; vis[x][y] = true; return dfs(x, y, 0); } private int dfs(int i, int j, int k) { if (grid[i][j] == 2) { return k == cnt + 1 ? 1 : 0; } int ans = 0; int[] dirs = {-1, 0, 1, 0, -1}; for (int h = 0; h < 4; ++h) { int x = i + dirs[h], y = j + dirs[h + 1]; if (x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && grid[x][y] != -1) { vis[x][y] = true; ans += dfs(x, y, k + 1); vis[x][y] = false; } } return ans; } } -
class Solution { public: int uniquePathsIII(vector<vector<int>>& grid) { int m = grid.size(), n = grid[0].size(); int cnt = 0; for (auto& row : grid) { for (auto& x : row) { cnt += x == 0; } } int dirs[5] = {-1, 0, 1, 0, -1}; bool vis[m][n]; memset(vis, false, sizeof vis); function<int(int, int, int)> dfs = [&](int i, int j, int k) -> int { if (grid[i][j] == 2) { return k == cnt + 1 ? 1 : 0; } int ans = 0; for (int h = 0; h < 4; ++h) { int x = i + dirs[h], y = j + dirs[h + 1]; if (x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && grid[x][y] != -1) { vis[x][y] = true; ans += dfs(x, y, k + 1); vis[x][y] = false; } } return ans; }; for (int i = 0; i < m; ++i) { for (int j = 0; j < n; ++j) { if (grid[i][j] == 1) { vis[i][j] = true; return dfs(i, j, 0); } } } return 0; } }; -
''' >>> ( (i,j) for i in range(3) for j in range(3) if i == j ) <generator object <genexpr> at 0x104da5150> >>> list( (i,j) for i in range(3) for j in range(3) if i == j ) [(0, 0), (1, 1), (2, 2)] >>> next( (i,j) for i in range(3) for j in range(3) if i == j ) (0, 0) basically next() is same as list()[0] ''' class Solution: # dfs def uniquePathsIII(self, grid: List[List[int]]) -> int: def dfs(i, j, k): if grid[i][j] == 2: return int(k == cnt + 1) ans = 0 for a, b in pairwise(dirs): x, y = i + a, j + b if 0 <= x < m and 0 <= y < n and (x, y) not in vis and grid[x][y] != -1: vis.add((x, y)) ans += dfs(x, y, k + 1) vis.remove((x, y)) # set() cannot pop(index) or pop(val), only pop() return ans m, n = len(grid), len(grid[0]) start = next((i, j) for i in range(m) for j in range(n) if grid[i][j] == 1) dirs = (-1, 0, 1, 0, -1) cnt = sum(grid[i][j] == 0 for i in range(m) for j in range(n)) vis = {start} # start here is a tuple (i,j) return dfs(*start, 0) # '*start' means that the elements of the start iterable are being unpacked # and passed as separate arguments to the dfs function ######## ''' >>> visited = set([(1,1),(2,2)]) >>> visited {(1, 1), (2, 2)} >>> >>> visited | {(3,3), (4,4)} {(4, 4), (1, 1), (3, 3), (2, 2)} ''' # 980. Unique Paths III # https://leetcode.com/problems/unique-paths-iii/ class Solution: # bfs def uniquePathsIII(self, grid: List[List[int]]) -> int: rows, cols = len(grid), len(grid[0]) available = 0 sx = sy = ex = ey = 0 # start x/y, end x/y res = 0 for x in range(rows): for y in range(cols): if grid[x][y] != -1: available += 1 if grid[x][y] == 1: sx, sy = x, y elif grid[x][y] == 2: ex, ey = x, y queue = deque([(sx, sy, 1, set([(sx, sy)]))]) # x, y, count, visited while queue: x, y, count, visited = queue.popleft() if x == ex and y == ey and count == available: res += 1 continue for dx, dy in [(x + 1, y), (x - 1, y), (x, y + 1), (x, y - 1)]: if 0 <= dx < rows and 0 <= dy < cols and grid[dx][dy] != -1 and count + 1 <= available and (dx, dy) not in visited: new_visited = visited | {(dx, dy)} # or just add() queue.append((dx, dy, count + 1, new_visited)) return res -
func uniquePathsIII(grid [][]int) int { m, n := len(grid), len(grid[0]) cnt := 0 vis := make([][]bool, m) x, y := 0, 0 for i, row := range grid { vis[i] = make([]bool, n) for j, v := range row { if v == 0 { cnt++ } else if v == 1 { x, y = i, j } } } dirs := [5]int{-1, 0, 1, 0, -1} var dfs func(i, j, k int) int dfs = func(i, j, k int) int { if grid[i][j] == 2 { if k == cnt+1 { return 1 } return 0 } ans := 0 for h := 0; h < 4; h++ { x, y := i+dirs[h], j+dirs[h+1] if x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && grid[x][y] != -1 { vis[x][y] = true ans += dfs(x, y, k+1) vis[x][y] = false } } return ans } vis[x][y] = true return dfs(x, y, 0) } -
function uniquePathsIII(grid: number[][]): number { const m = grid.length; const n = grid[0].length; let [x, y] = [0, 0]; let cnt = 0; for (let i = 0; i < m; ++i) { for (let j = 0; j < n; ++j) { if (grid[i][j] === 0) { ++cnt; } else if (grid[i][j] == 1) { [x, y] = [i, j]; } } } const vis: boolean[][] = Array(m) .fill(0) .map(() => Array(n).fill(false)); vis[x][y] = true; const dirs = [-1, 0, 1, 0, -1]; const dfs = (i: number, j: number, k: number): number => { if (grid[i][j] === 2) { return k === cnt + 1 ? 1 : 0; } let ans = 0; for (let d = 0; d < 4; ++d) { const [x, y] = [i + dirs[d], j + dirs[d + 1]]; if (x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && grid[x][y] !== -1) { vis[x][y] = true; ans += dfs(x, y, k + 1); vis[x][y] = false; } } return ans; }; return dfs(x, y, 0); }