Welcome to Subscribe On Youtube

965. Univalued Binary Tree

Description

A binary tree is uni-valued if every node in the tree has the same value.

Given the root of a binary tree, return true if the given tree is uni-valued, or false otherwise.

 

Example 1:

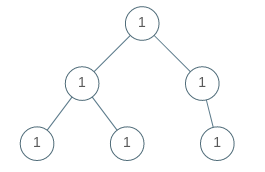
Input: root = [1,1,1,1,1,null,1]
Output: true

Example 2:

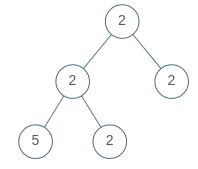
Input: root = [2,2,2,5,2]
Output: false

 

Constraints:

• The number of nodes in the tree is in the range [1, 100].
• 0 <= Node.val < 100

Solutions

• Java
• C++
• Python
• Go
• TypeScript
• RenderScript

• /**
   * Definition for a binary tree node.
   * public class TreeNode {
   *     int val;
   *     TreeNode left;
   *     TreeNode right;
   *     TreeNode() {}
   *     TreeNode(int val) { this.val = val; }
   *     TreeNode(int val, TreeNode left, TreeNode right) {
   *         this.val = val;
   *         this.left = left;
   *         this.right = right;
   *     }
   * }
   */
  class Solution {
      public boolean isUnivalTree(TreeNode root) {
          return dfs(root, root.val);
      }
  
      private boolean dfs(TreeNode root, int val) {
          if (root == null) {
              return true;
          }
          return root.val == val && dfs(root.left, val) && dfs(root.right, val);
      }
  }
  

• /**
   * Definition for a binary tree node.
   * struct TreeNode {
   *     int val;
   *     TreeNode *left;
   *     TreeNode *right;
   *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
   *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
   *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
   * };
   */
  class Solution {
  public:
      bool isUnivalTree(TreeNode* root) {
          return dfs(root, root->val);
      }
  
      bool dfs(TreeNode* root, int val) {
          if (!root) return true;
          return root->val == val && dfs(root->left, val) && dfs(root->right, val);
      }
  };
  

• # Definition for a binary tree node.
  # class TreeNode:
  #     def __init__(self, val=0, left=None, right=None):
  #         self.val = val
  #         self.left = left
  #         self.right = right
  class Solution:
      def isUnivalTree(self, root: TreeNode) -> bool:
          def dfs(node):
              if node is None:
                  return True
              return node.val == root.val and dfs(node.left) and dfs(node.right)
  
          return dfs(root)
  
  

• /**
   * Definition for a binary tree node.
   * type TreeNode struct {
   *     Val int
   *     Left *TreeNode
   *     Right *TreeNode
   * }
   */
  func isUnivalTree(root *TreeNode) bool {
  	var dfs func(*TreeNode) bool
  	dfs = func(node *TreeNode) bool {
  		if node == nil {
  			return true
  		}
  		return node.Val == root.Val && dfs(node.Left) && dfs(node.Right)
  	}
  	return dfs(root)
  }
  

• /**
   * Definition for a binary tree node.
   * class TreeNode {
   *     val: number
   *     left: TreeNode | null
   *     right: TreeNode | null
   *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
   *         this.val = (val===undefined ? 0 : val)
   *         this.left = (left===undefined ? null : left)
   *         this.right = (right===undefined ? null : right)
   *     }
   * }
   */
  
  function isUnivalTree(root: TreeNode | null): boolean {
      const val = root.val;
      const dfs = (root: TreeNode | null) => {
          if (root == null) {
              return true;
          }
          return root.val === val && dfs(root.left) && dfs(root.right);
      };
      return dfs(root.left) && dfs(root.right);
  }
  
  

• // Definition for a binary tree node.
  // #[derive(Debug, PartialEq, Eq)]
  // pub struct TreeNode {
  //   pub val: i32,
  //   pub left: Option<Rc<RefCell<TreeNode>>>,
  //   pub right: Option<Rc<RefCell<TreeNode>>>,
  // }
  //
  // impl TreeNode {
  //   #[inline]
  //   pub fn new(val: i32) -> Self {
  //     TreeNode {
  //       val,
  //       left: None,
  //       right: None
  //     }
  //   }
  // }
  use std::rc::Rc;
  use std::cell::RefCell;
  impl Solution {
      fn dfs(val: i32, root: &Option<Rc<RefCell<TreeNode>>>) -> bool {
          if root.is_none() {
              return true;
          }
          let root = root.as_ref().unwrap().borrow();
          root.val == val && Self::dfs(val, &root.left) && Self::dfs(val, &root.right)
      }
      pub fn is_unival_tree(root: Option<Rc<RefCell<TreeNode>>>) -> bool {
          let root = root.as_ref().unwrap().borrow();
          Self::dfs(root.val, &root.left) && Self::dfs(root.val, &root.right)
      }
  }
  
  

All Problems

All Solutions