Welcome to Subscribe On Youtube

952. Largest Component Size by Common Factor

Description

You are given an integer array of unique positive integers nums. Consider the following graph:

• There are nums.length nodes, labeled nums[0] to nums[nums.length - 1],
• There is an undirected edge between nums[i] and nums[j] if nums[i] and nums[j] share a common factor greater than 1.

Return the size of the largest connected component in the graph.

 

Example 1:

Input: nums = [4,6,15,35]
Output: 4

Example 2:

Input: nums = [20,50,9,63]
Output: 2

Example 3:

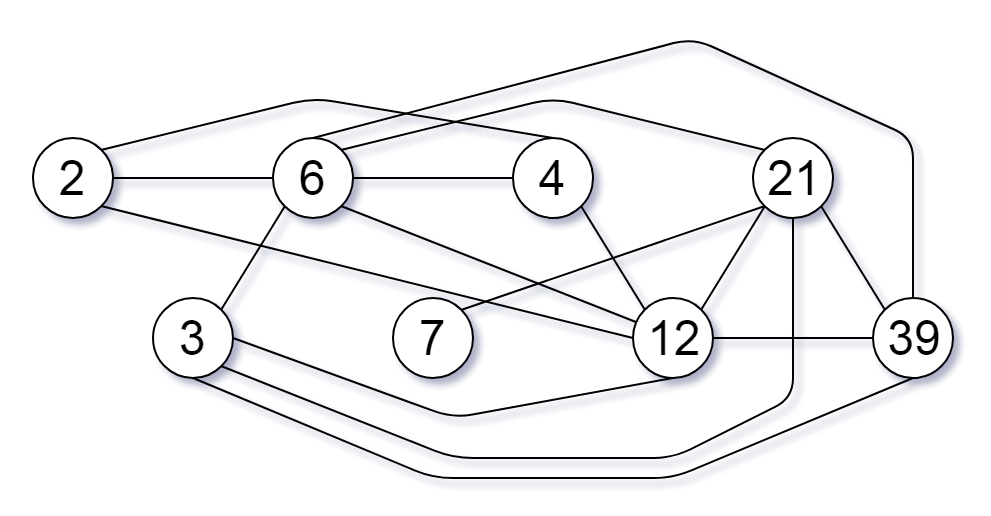
Input: nums = [2,3,6,7,4,12,21,39]
Output: 8

 

Constraints:

• 1 <= nums.length <= 2 * 104
• 1 <= nums[i] <= 105
• All the values of nums are unique.

Solutions

• Java
• C++
• Python
• Go

• class UnionFind {
      int[] p;
  
      UnionFind(int n) {
          p = new int[n];
          for (int i = 0; i < n; ++i) {
              p[i] = i;
          }
      }
  
      void union(int a, int b) {
          int pa = find(a), pb = find(b);
          if (pa != pb) {
              p[pa] = pb;
          }
      }
  
      int find(int x) {
          if (p[x] != x) {
              p[x] = find(p[x]);
          }
          return p[x];
      }
  }
  
  class Solution {
      public int largestComponentSize(int[] nums) {
          int m = 0;
          for (int v : nums) {
              m = Math.max(m, v);
          }
          UnionFind uf = new UnionFind(m + 1);
          for (int v : nums) {
              int i = 2;
              while (i <= v / i) {
                  if (v % i == 0) {
                      uf.union(v, i);
                      uf.union(v, v / i);
                  }
                  ++i;
              }
          }
          int[] cnt = new int[m + 1];
          int ans = 0;
          for (int v : nums) {
              int t = uf.find(v);
              ++cnt[t];
              ans = Math.max(ans, cnt[t]);
          }
          return ans;
      }
  }
  

• class UnionFind {
  public:
      vector<int> p;
      int n;
  
      UnionFind(int _n)
          : n(_n)
          , p(_n) {
          iota(p.begin(), p.end(), 0);
      }
  
      void unite(int a, int b) {
          int pa = find(a), pb = find(b);
          if (pa != pb) p[pa] = pb;
      }
  
      int find(int x) {
          if (p[x] != x) p[x] = find(p[x]);
          return p[x];
      }
  };
  
  class Solution {
  public:
      int largestComponentSize(vector<int>& nums) {
          int m = *max_element(nums.begin(), nums.end());
          UnionFind* uf = new UnionFind(m + 1);
          for (int v : nums) {
              int i = 2;
              while (i <= v / i) {
                  if (v % i == 0) {
                      uf->unite(v, i);
                      uf->unite(v, v / i);
                  }
                  ++i;
              }
          }
          vector<int> cnt(m + 1);
          int ans = 0;
          for (int v : nums) {
              int t = uf->find(v);
              ++cnt[t];
              ans = max(ans, cnt[t]);
          }
          return ans;
      }
  };
  

• class UnionFind:
      def __init__(self, n):
          self.p = list(range(n))
  
      def union(self, a, b):
          pa, pb = self.find(a), self.find(b)
          if pa != pb:
              self.p[pa] = pb
  
      def find(self, x):
          if self.p[x] != x:
              self.p[x] = self.find(self.p[x])
          return self.p[x]
  
  
  class Solution:
      def largestComponentSize(self, nums: List[int]) -> int:
          uf = UnionFind(max(nums) + 1)
          for v in nums:
              i = 2
              while i <= v // i:
                  if v % i == 0:
                      uf.union(v, i)
                      uf.union(v, v // i)
                  i += 1
          return max(Counter(uf.find(v) for v in nums).values())
  
  

• func largestComponentSize(nums []int) int {
  	m := slices.Max(nums)
  	p := make([]int, m+1)
  	for i := range p {
  		p[i] = i
  	}
  	var find func(int) int
  	find = func(x int) int {
  		if p[x] != x {
  			p[x] = find(p[x])
  		}
  		return p[x]
  	}
  	union := func(a, b int) {
  		pa, pb := find(a), find(b)
  		if pa != pb {
  			p[pa] = pb
  		}
  	}
  	for _, v := range nums {
  		i := 2
  		for i <= v/i {
  			if v%i == 0 {
  				union(v, i)
  				union(v, v/i)
  			}
  			i++
  		}
  	}
  	cnt := make([]int, m+1)
  	for _, v := range nums {
  		t := find(v)
  		cnt[t]++
  	}
  	return slices.Max(cnt)
  }
  

All Problems

All Solutions