Welcome to Subscribe On Youtube
938. Range Sum of BST
Description
Given the root node of a binary search tree and two integers low and high, return the sum of values of all nodes with a value in the inclusive range [low, high].
Example 1:
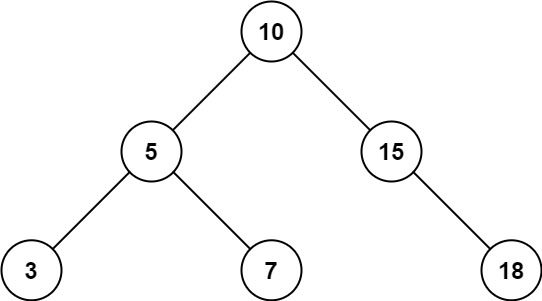
Input: root = [10,5,15,3,7,null,18], low = 7, high = 15 Output: 32 Explanation: Nodes 7, 10, and 15 are in the range [7, 15]. 7 + 10 + 15 = 32.
Example 2:
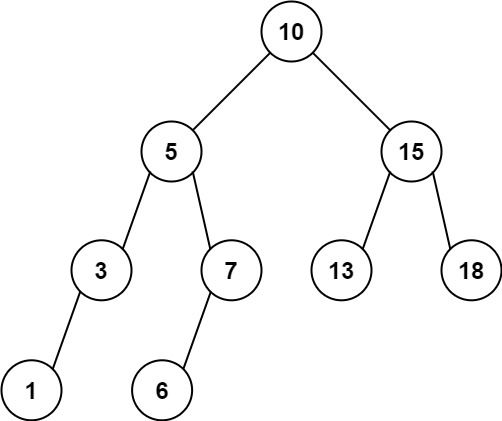
Input: root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10 Output: 23 Explanation: Nodes 6, 7, and 10 are in the range [6, 10]. 6 + 7 + 10 = 23.
Constraints:
- The number of nodes in the tree is in the range
[1, 2 * 104]. 1 <= Node.val <= 1051 <= low <= high <= 105- All
Node.valare unique.
Solutions
-
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { public int rangeSumBST(TreeNode root, int low, int high) { if (root == null) { return 0; } if (low <= root.val && root.val <= high) { return root.val + rangeSumBST(root.left, low, high) + rangeSumBST(root.right, low, high); } else if (root.val < low) { return rangeSumBST(root.right, low, high); } else { return rangeSumBST(root.left, low, high); } } } -
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: int rangeSumBST(TreeNode* root, int low, int high) { if (root == nullptr) return 0; if (low <= root->val && root->val <= high) { return root->val + rangeSumBST(root->left, low, high) + rangeSumBST(root->right, low, high); } else if (root->val < low) { return rangeSumBST(root->right, low, high); } else { return rangeSumBST(root->left, low, high); } } }; -
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def rangeSumBST(self, root: TreeNode, low: int, high: int) -> int: def search(node): if not node: return if low <= node.val <= high: self.ans += node.val search(node.left) search(node.right) elif node.val < low: search(node.right) elif node.val > high: search(node.left) self.ans = 0 search(root) return self.ans -
/** * Definition for a binary tree node. * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */ func rangeSumBST(root *TreeNode, low int, high int) int { if root == nil { return 0 } if low <= root.Val && root.Val <= high { return root.Val + rangeSumBST(root.Left, low, high) + rangeSumBST(root.Right, low, high) } else if root.Val < low { return rangeSumBST(root.Right, low, high) } else { return rangeSumBST(root.Left, low, high) } } -
/** * Definition for a binary tree node. * class TreeNode { * val: number * left: TreeNode | null * right: TreeNode | null * constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } * } */ function rangeSumBST(root: TreeNode | null, low: number, high: number): number { const dfs = (root: TreeNode | null): number => { if (!root) { return 0; } const { val, left, right } = root; let ans = low <= val && val <= high ? val : 0; if (val > low) { ans += dfs(left); } if (val < high) { ans += dfs(right); } return ans; }; return dfs(root); } -
/** * Definition for a binary tree node. * public class TreeNode { * public int val; * public TreeNode left; * public TreeNode right; * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) { * this.val = val; * this.left = left; * this.right = right; * } * } */ public class Solution { public int RangeSumBST(TreeNode root, int low, int high) { return dfs(root, low, high); } private int dfs(TreeNode root, int low, int high) { if (root == null) { return 0; } int x = root.val; int ans = low <= x && x <= high ? x : 0; if (x > low) { ans += dfs(root.left, low, high); } if (x < high) { ans += dfs(root.right, low, high); } return ans; } }