Welcome to Subscribe On Youtube

892. Surface Area of 3D Shapes

Description

You are given an n x n grid where you have placed some 1 x 1 x 1 cubes. Each value v = grid[i][j] represents a tower of v cubes placed on top of cell (i, j).

After placing these cubes, you have decided to glue any directly adjacent cubes to each other, forming several irregular 3D shapes.

Return the total surface area of the resulting shapes.

Note: The bottom face of each shape counts toward its surface area.

 

Example 1:

Input: grid = [[1,2],[3,4]]
Output: 34

Example 2:

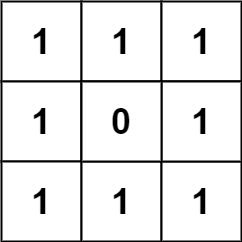
Input: grid = [[1,1,1],[1,0,1],[1,1,1]]
Output: 32

Example 3:

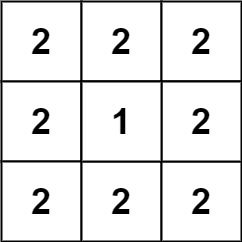
Input: grid = [[2,2,2],[2,1,2],[2,2,2]]
Output: 46

 

Constraints:

• n == grid.length == grid[i].length
• 1 <= n <= 50
• 0 <= grid[i][j] <= 50

Solutions

• Java
• C++
• Python
• Go

• class Solution {
      public int surfaceArea(int[][] grid) {
          int n = grid.length;
          int ans = 0;
          for (int i = 0; i < n; ++i) {
              for (int j = 0; j < n; ++j) {
                  if (grid[i][j] > 0) {
                      ans += 2 + grid[i][j] * 4;
                      if (i > 0) {
                          ans -= Math.min(grid[i][j], grid[i - 1][j]) * 2;
                      }
                      if (j > 0) {
                          ans -= Math.min(grid[i][j], grid[i][j - 1]) * 2;
                      }
                  }
              }
          }
          return ans;
      }
  }
  

• class Solution {
  public:
      int surfaceArea(vector<vector<int>>& grid) {
          int n = grid.size();
          int ans = 0;
          for (int i = 0; i < n; ++i) {
              for (int j = 0; j < n; ++j) {
                  if (grid[i][j]) {
                      ans += 2 + grid[i][j] * 4;
                      if (i) ans -= min(grid[i][j], grid[i - 1][j]) * 2;
                      if (j) ans -= min(grid[i][j], grid[i][j - 1]) * 2;
                  }
              }
          }
          return ans;
      }
  };
  

• class Solution:
      def surfaceArea(self, grid: List[List[int]]) -> int:
          ans = 0
          for i, row in enumerate(grid):
              for j, v in enumerate(row):
                  if v:
                      ans += 2 + v * 4
                      if i:
                          ans -= min(v, grid[i - 1][j]) * 2
                      if j:
                          ans -= min(v, grid[i][j - 1]) * 2
          return ans
  
  

• func surfaceArea(grid [][]int) int {
  	ans := 0
  	for i, row := range grid {
  		for j, v := range row {
  			if v > 0 {
  				ans += 2 + v*4
  				if i > 0 {
  					ans -= min(v, grid[i-1][j]) * 2
  				}
  				if j > 0 {
  					ans -= min(v, grid[i][j-1]) * 2
  				}
  			}
  		}
  	}
  	return ans
  }
  

All Problems

All Solutions