Welcome to Subscribe On Youtube
863. All Nodes Distance K in Binary Tree
Description
Given the root of a binary tree, the value of a target node target, and an integer k, return an array of the values of all nodes that have a distance k from the target node.
You can return the answer in any order.
Example 1:
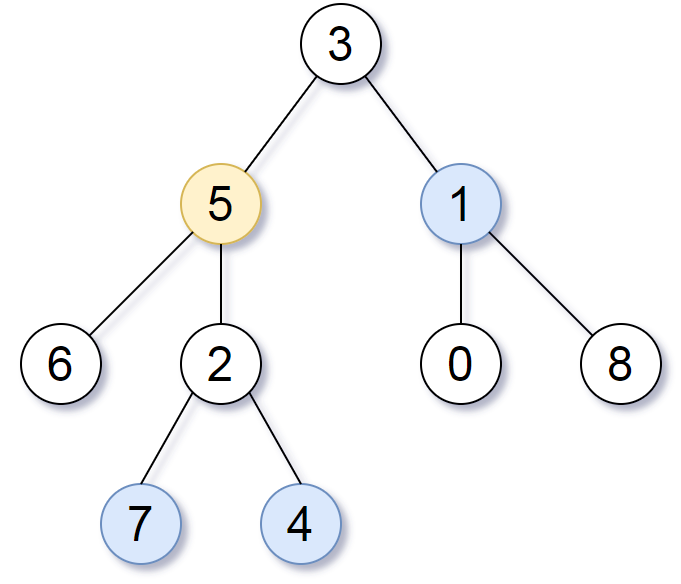
Input: root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, k = 2 Output: [7,4,1] Explanation: The nodes that are a distance 2 from the target node (with value 5) have values 7, 4, and 1.
Example 2:
Input: root = [1], target = 1, k = 3 Output: []
Constraints:
- The number of nodes in the tree is in the range
[1, 500]. 0 <= Node.val <= 500- All the values
Node.valare unique. targetis the value of one of the nodes in the tree.0 <= k <= 1000
Solutions
-
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */ class Solution { private Map<TreeNode, TreeNode> p; private Set<Integer> vis; private List<Integer> ans; public List<Integer> distanceK(TreeNode root, TreeNode target, int k) { p = new HashMap<>(); vis = new HashSet<>(); ans = new ArrayList<>(); parents(root, null); dfs(target, k); return ans; } private void parents(TreeNode root, TreeNode prev) { if (root == null) { return; } p.put(root, prev); parents(root.left, root); parents(root.right, root); } private void dfs(TreeNode root, int k) { if (root == null || vis.contains(root.val)) { return; } vis.add(root.val); if (k == 0) { ans.add(root.val); return; } dfs(root.left, k - 1); dfs(root.right, k - 1); dfs(p.get(root), k - 1); } } -
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode(int x) : val(x), left(NULL), right(NULL) {} * }; */ class Solution { public: unordered_map<TreeNode*, TreeNode*> p; unordered_set<int> vis; vector<int> ans; vector<int> distanceK(TreeNode* root, TreeNode* target, int k) { parents(root, nullptr); dfs(target, k); return ans; } void parents(TreeNode* root, TreeNode* prev) { if (!root) return; p[root] = prev; parents(root->left, root); parents(root->right, root); } void dfs(TreeNode* root, int k) { if (!root || vis.count(root->val)) return; vis.insert(root->val); if (k == 0) { ans.push_back(root->val); return; } dfs(root->left, k - 1); dfs(root->right, k - 1); dfs(p[root], k - 1); } }; -
# Definition for a binary tree node. # class TreeNode: # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution: def distanceK(self, root: TreeNode, target: TreeNode, k: int) -> List[int]: def parents(root, prev): nonlocal p if root is None: return p[root] = prev parents(root.left, root) parents(root.right, root) def dfs(root, k): nonlocal ans, vis if root is None or root.val in vis: return vis.add(root.val) if k == 0: ans.append(root.val) return dfs(root.left, k - 1) dfs(root.right, k - 1) dfs(p[root], k - 1) p = {} parents(root, None) ans = [] vis = set() dfs(target, k) return ans -
/** * Definition for a binary tree node. * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */ func distanceK(root *TreeNode, target *TreeNode, k int) []int { p := make(map[*TreeNode]*TreeNode) vis := make(map[int]bool) var ans []int var parents func(root, prev *TreeNode) parents = func(root, prev *TreeNode) { if root == nil { return } p[root] = prev parents(root.Left, root) parents(root.Right, root) } parents(root, nil) var dfs func(root *TreeNode, k int) dfs = func(root *TreeNode, k int) { if root == nil || vis[root.Val] { return } vis[root.Val] = true if k == 0 { ans = append(ans, root.Val) return } dfs(root.Left, k-1) dfs(root.Right, k-1) dfs(p[root], k-1) } dfs(target, k) return ans } -
/** * Definition for a binary tree node. * class TreeNode { * val: number * left: TreeNode | null * right: TreeNode | null * constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } * } */ function distanceK(root: TreeNode | null, target: TreeNode | null, k: number): number[] { if (!root) return [0]; const g: Record<number, number[]> = {}; const dfs = (node: TreeNode | null, parent: TreeNode | null = null) => { if (!node) return; g[node.val] ??= []; if (parent) g[node.val].push(parent.val); if (node.left) g[node.val].push(node.left.val); if (node.right) g[node.val].push(node.right.val); dfs(node.left, node); dfs(node.right, node); }; dfs(root); const vis = new Set<number>(); let q = [target!.val]; while (q.length) { if (!k--) return q; const nextQ: number[] = []; for (const x of q) { if (vis.has(x)) continue; vis.add(x); nextQ.push(...g[x].filter(x => !vis.has(x))); } q = nextQ; } return []; }