Welcome to Subscribe On Youtube
850. Rectangle Area II
Description
You are given a 2D array of axis-aligned rectangles. Each rectangle[i] = [xi1, yi1, xi2, yi2] denotes the ith rectangle where (xi1, yi1) are the coordinates of the bottom-left corner, and (xi2, yi2) are the coordinates of the top-right corner.
Calculate the total area covered by all rectangles in the plane. Any area covered by two or more rectangles should only be counted once.
Return the total area. Since the answer may be too large, return it modulo 109 + 7.
Example 1:
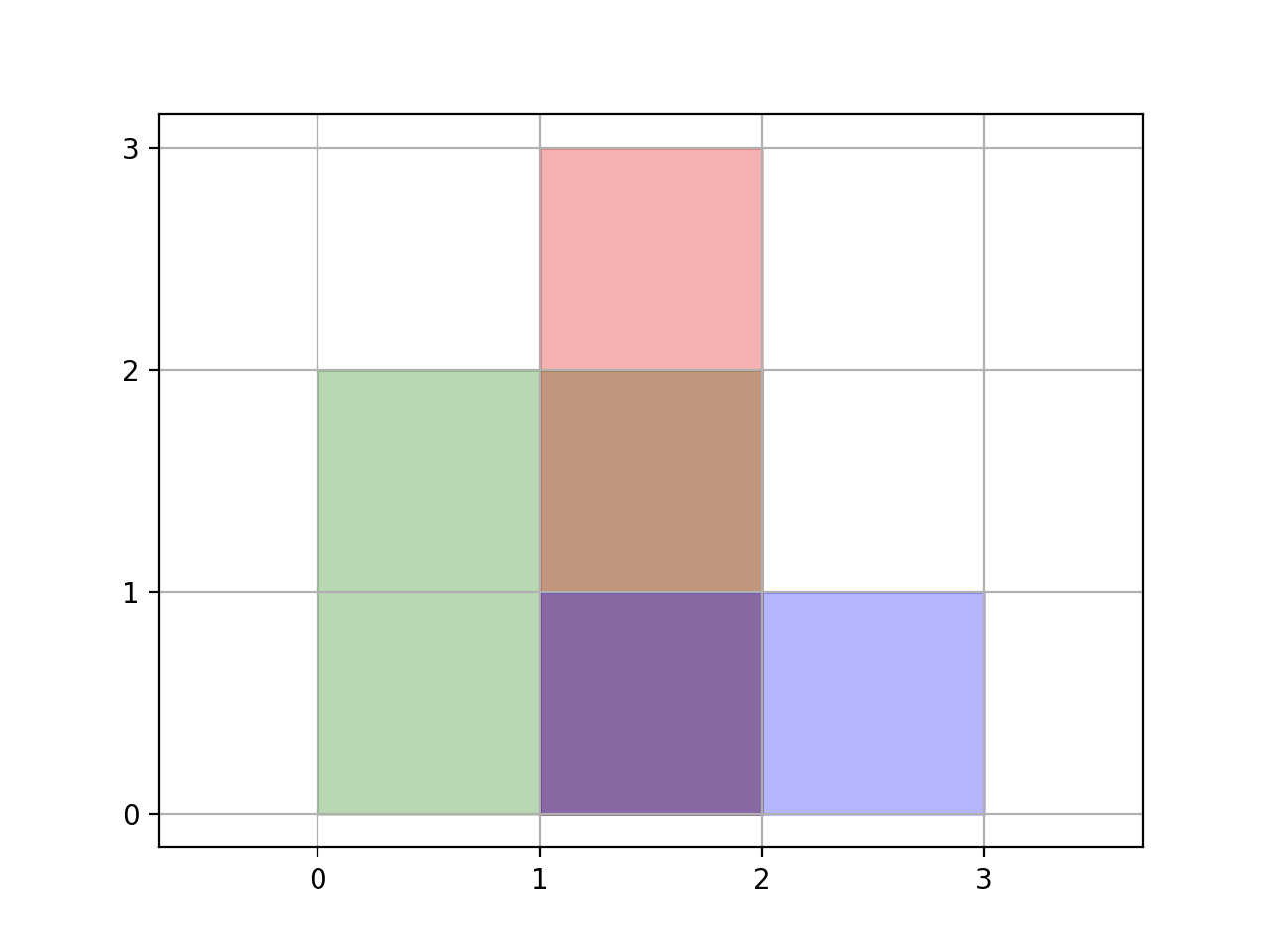
Input: rectangles = [[0,0,2,2],[1,0,2,3],[1,0,3,1]] Output: 6 Explanation: A total area of 6 is covered by all three rectangles, as illustrated in the picture. From (1,1) to (2,2), the green and red rectangles overlap. From (1,0) to (2,3), all three rectangles overlap.
Example 2:
Input: rectangles = [[0,0,1000000000,1000000000]] Output: 49 Explanation: The answer is 1018 modulo (109 + 7), which is 49.
Constraints:
1 <= rectangles.length <= 200rectanges[i].length == 40 <= xi1, yi1, xi2, yi2 <= 109xi1 <= xi2yi1 <= yi2
Solutions
-
class Node { int l, r, cnt, length; } class SegmentTree { private Node[] tr; private int[] nums; public SegmentTree(int[] nums) { this.nums = nums; int n = nums.length - 1; tr = new Node[n << 2]; for (int i = 0; i < tr.length; ++i) { tr[i] = new Node(); } build(1, 0, n - 1); } private void build(int u, int l, int r) { tr[u].l = l; tr[u].r = r; if (l != r) { int mid = (l + r) >> 1; build(u << 1, l, mid); build(u << 1 | 1, mid + 1, r); } } public void modify(int u, int l, int r, int k) { if (tr[u].l >= l && tr[u].r <= r) { tr[u].cnt += k; } else { int mid = (tr[u].l + tr[u].r) >> 1; if (l <= mid) { modify(u << 1, l, r, k); } if (r > mid) { modify(u << 1 | 1, l, r, k); } } pushup(u); } private void pushup(int u) { if (tr[u].cnt > 0) { tr[u].length = nums[tr[u].r + 1] - nums[tr[u].l]; } else if (tr[u].l == tr[u].r) { tr[u].length = 0; } else { tr[u].length = tr[u << 1].length + tr[u << 1 | 1].length; } } public int query() { return tr[1].length; } } class Solution { private static final int MOD = (int) 1e9 + 7; public int rectangleArea(int[][] rectangles) { int n = rectangles.length; int[][] segs = new int[n << 1][4]; int i = 0; TreeSet<Integer> ts = new TreeSet<>(); for (var e : rectangles) { int x1 = e[0], y1 = e[1], x2 = e[2], y2 = e[3]; segs[i++] = new int[] {x1, y1, y2, 1}; segs[i++] = new int[] {x2, y1, y2, -1}; ts.add(y1); ts.add(y2); } Arrays.sort(segs, (a, b) -> a[0] - b[0]); Map<Integer, Integer> m = new HashMap<>(ts.size()); i = 0; int[] nums = new int[ts.size()]; for (int v : ts) { m.put(v, i); nums[i++] = v; } SegmentTree tree = new SegmentTree(nums); long ans = 0; for (i = 0; i < segs.length; ++i) { var e = segs[i]; int x = e[0], y1 = e[1], y2 = e[2], k = e[3]; if (i > 0) { ans += (long) tree.query() * (x - segs[i - 1][0]); } tree.modify(1, m.get(y1), m.get(y2) - 1, k); } ans %= MOD; return (int) ans; } } -
class Node { public: int l, r, cnt, length; }; class SegmentTree { public: vector<Node*> tr; vector<int> nums; SegmentTree(vector<int>& nums) { this->nums = nums; int n = nums.size() - 1; tr.resize(n << 2); for (int i = 0; i < tr.size(); ++i) tr[i] = new Node(); build(1, 0, n - 1); } void build(int u, int l, int r) { tr[u]->l = l; tr[u]->r = r; if (l != r) { int mid = (l + r) >> 1; build(u << 1, l, mid); build(u << 1 | 1, mid + 1, r); } } void modify(int u, int l, int r, int k) { if (tr[u]->l >= l && tr[u]->r <= r) tr[u]->cnt += k; else { int mid = (tr[u]->l + tr[u]->r) >> 1; if (l <= mid) modify(u << 1, l, r, k); if (r > mid) modify(u << 1 | 1, l, r, k); } pushup(u); } int query() { return tr[1]->length; } void pushup(int u) { if (tr[u]->cnt) tr[u]->length = nums[tr[u]->r + 1] - nums[tr[u]->l]; else if (tr[u]->l == tr[u]->r) tr[u]->length = 0; else tr[u]->length = tr[u << 1]->length + tr[u << 1 | 1]->length; } }; class Solution { public: const int mod = 1e9 + 7; int rectangleArea(vector<vector<int>>& rectangles) { int n = rectangles.size(); vector<vector<int>> segs(n << 1); set<int> ts; int i = 0; for (auto& e : rectangles) { int x1 = e[0], y1 = e[1], x2 = e[2], y2 = e[3]; segs[i++] = {x1, y1, y2, 1}; segs[i++] = {x2, y1, y2, -1}; ts.insert(y1); ts.insert(y2); } sort(segs.begin(), segs.end()); unordered_map<int, int> m; i = 0; for (int v : ts) m[v] = i++; vector<int> nums(ts.begin(), ts.end()); SegmentTree* tree = new SegmentTree(nums); long long ans = 0; for (int i = 0; i < segs.size(); ++i) { auto e = segs[i]; int x = e[0], y1 = e[1], y2 = e[2], k = e[3]; if (i > 0) ans += (long long) tree->query() * (x - segs[i - 1][0]); tree->modify(1, m[y1], m[y2] - 1, k); } ans %= mod; return (int) ans; } }; -
class Node: def __init__(self): self.l = self.r = 0 self.cnt = self.length = 0 class SegmentTree: def __init__(self, nums): n = len(nums) - 1 self.nums = nums self.tr = [Node() for _ in range(n << 2)] self.build(1, 0, n - 1) def build(self, u, l, r): self.tr[u].l, self.tr[u].r = l, r if l != r: mid = (l + r) >> 1 self.build(u << 1, l, mid) self.build(u << 1 | 1, mid + 1, r) def modify(self, u, l, r, k): if self.tr[u].l >= l and self.tr[u].r <= r: self.tr[u].cnt += k else: mid = (self.tr[u].l + self.tr[u].r) >> 1 if l <= mid: self.modify(u << 1, l, r, k) if r > mid: self.modify(u << 1 | 1, l, r, k) self.pushup(u) def pushup(self, u): if self.tr[u].cnt: self.tr[u].length = self.nums[self.tr[u].r + 1] - self.nums[self.tr[u].l] elif self.tr[u].l == self.tr[u].r: self.tr[u].length = 0 else: self.tr[u].length = self.tr[u << 1].length + self.tr[u << 1 | 1].length @property def length(self): return self.tr[1].length class Solution: def rectangleArea(self, rectangles: List[List[int]]) -> int: segs = [] alls = set() for x1, y1, x2, y2 in rectangles: segs.append((x1, y1, y2, 1)) segs.append((x2, y1, y2, -1)) alls.update([y1, y2]) segs.sort() alls = sorted(alls) tree = SegmentTree(alls) m = {v: i for i, v in enumerate(alls)} ans = 0 for i, (x, y1, y2, k) in enumerate(segs): if i: ans += tree.length * (x - segs[i - 1][0]) tree.modify(1, m[y1], m[y2] - 1, k) ans %= int(1e9 + 7) return ans -
func rectangleArea(rectangles [][]int) int { var mod int = 1e9 + 7 segs := [][]int{} alls := map[int]bool{} for _, e := range rectangles { x1, y1, x2, y2 := e[0], e[1], e[2], e[3] segs = append(segs, []int{x1, y1, y2, 1}) segs = append(segs, []int{x2, y1, y2, -1}) alls[y1] = true alls[y2] = true } nums := []int{} for v := range alls { nums = append(nums, v) } sort.Ints(nums) sort.Slice(segs, func(i, j int) bool { return segs[i][0] < segs[j][0] }) m := map[int]int{} for i, v := range nums { m[v] = i } tree := newSegmentTree(nums) ans := 0 for i, e := range segs { x, y1, y2, k := e[0], e[1], e[2], e[3] if i > 0 { ans += tree.query() * (x - segs[i-1][0]) ans %= mod } tree.modify(1, m[y1], m[y2]-1, k) } return ans } type node struct { l int r int cnt int length int } type segmentTree struct { tr []*node nums []int } func newSegmentTree(nums []int) *segmentTree { n := len(nums) - 1 tr := make([]*node, n<<2) for i := range tr { tr[i] = &node{} } t := &segmentTree{tr, nums} t.build(1, 0, n-1) return t } func (t *segmentTree) build(u, l, r int) { t.tr[u].l, t.tr[u].r = l, r if l == r { return } mid := (l + r) >> 1 t.build(u<<1, l, mid) t.build(u<<1|1, mid+1, r) } func (t *segmentTree) modify(u, l, r, k int) { if t.tr[u].l >= l && t.tr[u].r <= r { t.tr[u].cnt += k } else { mid := (t.tr[u].l + t.tr[u].r) >> 1 if l <= mid { t.modify(u<<1, l, r, k) } if r > mid { t.modify(u<<1|1, l, r, k) } } t.pushup(u) } func (t *segmentTree) query() int { return t.tr[1].length } func (t *segmentTree) pushup(u int) { if t.tr[u].cnt > 0 { t.tr[u].length = t.nums[t.tr[u].r+1] - t.nums[t.tr[u].l] } else if t.tr[u].l == t.tr[u].r { t.tr[u].length = 0 } else { t.tr[u].length = t.tr[u<<1].length + t.tr[u<<1|1].length } }