Welcome to Subscribe On Youtube
838. Push Dominoes
Description
There are n dominoes in a line, and we place each domino vertically upright. In the beginning, we simultaneously push some of the dominoes either to the left or to the right.
After each second, each domino that is falling to the left pushes the adjacent domino on the left. Similarly, the dominoes falling to the right push their adjacent dominoes standing on the right.
When a vertical domino has dominoes falling on it from both sides, it stays still due to the balance of the forces.
For the purposes of this question, we will consider that a falling domino expends no additional force to a falling or already fallen domino.
You are given a string dominoes representing the initial state where:
dominoes[i] = 'L', if theithdomino has been pushed to the left,dominoes[i] = 'R', if theithdomino has been pushed to the right, anddominoes[i] = '.', if theithdomino has not been pushed.
Return a string representing the final state.
Example 1:
Input: dominoes = "RR.L" Output: "RR.L" Explanation: The first domino expends no additional force on the second domino.
Example 2:
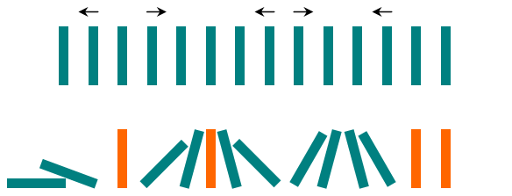
Input: dominoes = ".L.R...LR..L.." Output: "LL.RR.LLRRLL.."
Constraints:
n == dominoes.length1 <= n <= 105dominoes[i]is either'L','R', or'.'.
Solutions
-
public class Solution { public String pushDominoes(String dominoes) { int n = dominoes.length(); Deque<Integer> q = new ArrayDeque<>(); int[] time = new int[n]; Arrays.fill(time, -1); List<Character>[] force = new List[n]; for (int i = 0; i < n; ++i) { force[i] = new ArrayList<>(); } for (int i = 0; i < n; ++i) { char f = dominoes.charAt(i); if (f != '.') { q.offer(i); time[i] = 0; force[i].add(f); } } char[] ans = new char[n]; Arrays.fill(ans, '.'); while (!q.isEmpty()) { int i = q.poll(); if (force[i].size() == 1) { ans[i] = force[i].get(0); char f = ans[i]; int j = f == 'L' ? i - 1 : i + 1; if (j >= 0 && j < n) { int t = time[i]; if (time[j] == -1) { q.offer(j); time[j] = t + 1; force[j].add(f); } else if (time[j] == t + 1) { force[j].add(f); } } } } return new String(ans); } } class Solution {} -
class Solution { public: string pushDominoes(string dominoes) { int n = dominoes.size(); queue<int> q; vector<int> time(n, -1); vector<string> force(n); for (int i = 0; i < n; i++) { if (dominoes[i] == '.') continue; q.emplace(i); time[i] = 0; force[i].push_back(dominoes[i]); } string ans(n, '.'); while (!q.empty()) { int i = q.front(); q.pop(); if (force[i].size() == 1) { char f = force[i][0]; ans[i] = f; int j = (f == 'L') ? (i - 1) : (i + 1); if (j >= 0 && j < n) { int t = time[i]; if (time[j] == -1) { q.emplace(j); time[j] = t + 1; force[j].push_back(f); } else if (time[j] == t + 1) force[j].push_back(f); } } } return ans; } }; -
class Solution: def pushDominoes(self, dominoes: str) -> str: n = len(dominoes) q = deque() time = [-1] * n force = defaultdict(list) for i, f in enumerate(dominoes): if f != '.': q.append(i) time[i] = 0 force[i].append(f) ans = ['.'] * n while q: i = q.popleft() if len(force[i]) == 1: ans[i] = f = force[i][0] j = i - 1 if f == 'L' else i + 1 if 0 <= j < n: t = time[i] if time[j] == -1: q.append(j) time[j] = t + 1 force[j].append(f) elif time[j] == t + 1: force[j].append(f) return ''.join(ans) -
func pushDominoes(dominoes string) string { n := len(dominoes) q := []int{} time := make([]int, n) for i := range time { time[i] = -1 } force := make([][]byte, n) for i, c := range dominoes { if c != '.' { q = append(q, i) time[i] = 0 force[i] = append(force[i], byte(c)) } } ans := bytes.Repeat([]byte{'.'}, n) for len(q) > 0 { i := q[0] q = q[1:] if len(force[i]) > 1 { continue } f := force[i][0] ans[i] = f j := i - 1 if f == 'R' { j = i + 1 } if 0 <= j && j < n { t := time[i] if time[j] == -1 { q = append(q, j) time[j] = t + 1 force[j] = append(force[j], f) } else if time[j] == t+1 { force[j] = append(force[j], f) } } } return string(ans) } -
function pushDominoes(dominoes: string): string { const n = dominoes.length; const map = { L: -1, R: 1, '.': 0, }; let ans = new Array(n).fill(0); let visited = new Array(n).fill(0); let queue = []; let depth = 1; for (let i = 0; i < n; i++) { let cur = map[dominoes.charAt(i)]; if (cur) { queue.push(i); visited[i] = depth; ans[i] = cur; } } while (queue.length) { depth++; let nextLevel = []; for (let i of queue) { const dx = ans[i]; let x = i + dx; if (x >= 0 && x < n && [0, depth].includes(visited[x])) { ans[x] += dx; visited[x] = depth; nextLevel.push(x); } } queue = nextLevel; } return ans .map(d => { if (!d) return '.'; else if (d < 0) return 'L'; else return 'R'; }) .join(''); }