Welcome to Subscribe On Youtube
835. Image Overlap
Description
You are given two images, img1 and img2, represented as binary, square matrices of size n x n. A binary matrix has only 0s and 1s as values.
We translate one image however we choose by sliding all the 1 bits left, right, up, and/or down any number of units. We then place it on top of the other image. We can then calculate the overlap by counting the number of positions that have a 1 in both images.
Note also that a translation does not include any kind of rotation. Any 1 bits that are translated outside of the matrix borders are erased.
Return the largest possible overlap.
Example 1:
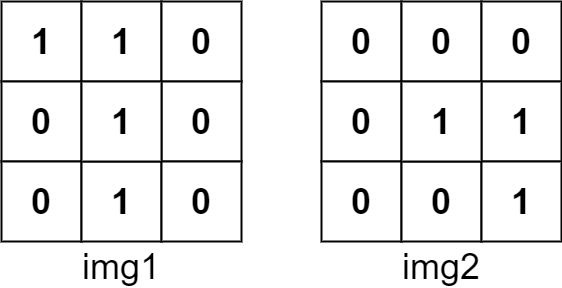
Input: img1 = [[1,1,0],[0,1,0],[0,1,0]], img2 = [[0,0,0],[0,1,1],[0,0,1]] Output: 3 Explanation: We translate img1 to right by 1 unit and down by 1 unit.The number of positions that have a 1 in both images is 3 (shown in red).

Example 2:
Input: img1 = [[1]], img2 = [[1]] Output: 1
Example 3:
Input: img1 = [[0]], img2 = [[0]] Output: 0
Constraints:
n == img1.length == img1[i].lengthn == img2.length == img2[i].length1 <= n <= 30img1[i][j]is either0or1.img2[i][j]is either0or1.
Solutions
-
class Solution { public int largestOverlap(int[][] img1, int[][] img2) { int n = img1.length; Map<List<Integer>, Integer> cnt = new HashMap<>(); int ans = 0; for (int i = 0; i < n; ++i) { for (int j = 0; j < n; ++j) { if (img1[i][j] == 1) { for (int h = 0; h < n; ++h) { for (int k = 0; k < n; ++k) { if (img2[h][k] == 1) { List<Integer> t = List.of(i - h, j - k); ans = Math.max(ans, cnt.merge(t, 1, Integer::sum)); } } } } } } return ans; } } -
class Solution { public: int largestOverlap(vector<vector<int>>& img1, vector<vector<int>>& img2) { int n = img1.size(); map<pair<int, int>, int> cnt; int ans = 0; for (int i = 0; i < n; ++i) { for (int j = 0; j < n; ++j) { if (img1[i][j]) { for (int h = 0; h < n; ++h) { for (int k = 0; k < n; ++k) { if (img2[h][k]) { ans = max(ans, ++cnt[{i - h, j - k}]); } } } } } } return ans; } }; -
class Solution: def largestOverlap(self, img1: List[List[int]], img2: List[List[int]]) -> int: n = len(img1) cnt = Counter() for i in range(n): for j in range(n): if img1[i][j]: for h in range(n): for k in range(n): if img2[h][k]: cnt[(i - h, j - k)] += 1 return max(cnt.values()) if cnt else 0 -
func largestOverlap(img1 [][]int, img2 [][]int) (ans int) { type pair struct{ x, y int } cnt := map[pair]int{} for i, row1 := range img1 { for j, x1 := range row1 { if x1 == 1 { for h, row2 := range img2 { for k, x2 := range row2 { if x2 == 1 { t := pair{i - h, j - k} cnt[t]++ ans = max(ans, cnt[t]) } } } } } } return } -
function largestOverlap(img1: number[][], img2: number[][]): number { const n = img1.length; const cnt: Map<number, number> = new Map(); let ans = 0; for (let i = 0; i < n; ++i) { for (let j = 0; j < n; ++j) { if (img1[i][j] === 1) { for (let h = 0; h < n; ++h) { for (let k = 0; k < n; ++k) { if (img2[h][k] === 1) { const t = (i - h) * 200 + (j - k); cnt.set(t, (cnt.get(t) ?? 0) + 1); ans = Math.max(ans, cnt.get(t)!); } } } } } } return ans; }