Welcome to Subscribe On Youtube

797. All Paths From Source to Target

Description

Given a directed acyclic graph (DAG) of n nodes labeled from 0 to n - 1, find all possible paths from node 0 to node n - 1 and return them in any order.

The graph is given as follows: graph[i] is a list of all nodes you can visit from node i (i.e., there is a directed edge from node i to node graph[i][j]).

 

Example 1:

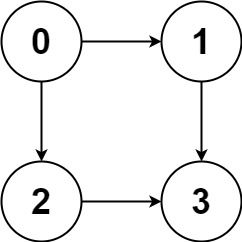
Input: graph = [[1,2],[3],[3],[]]
Output: [[0,1,3],[0,2,3]]
Explanation: There are two paths: 0 -> 1 -> 3 and 0 -> 2 -> 3.

Example 2:

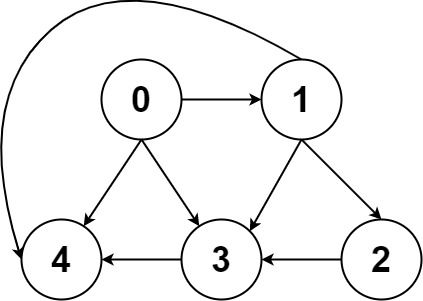
Input: graph = [[4,3,1],[3,2,4],[3],[4],[]]
Output: [[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

 

Constraints:

• n == graph.length
• 2 <= n <= 15
• 0 <= graph[i][j] < n
• graph[i][j] != i (i.e., there will be no self-loops).
• All the elements of graph[i] are unique.
• The input graph is guaranteed to be a DAG.

Solutions

Since there is no ring in the graph, you can simply use DFS or BFS to traverse it.

• Java
• C++
• Python
• Go
• Javascript
• RenderScript
• TypeScript

• class Solution {
      public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
          int n = graph.length;
          Queue<List<Integer>> queue = new ArrayDeque<>();
          queue.offer(Arrays.asList(0));
          List<List<Integer>> ans = new ArrayList<>();
          while (!queue.isEmpty()) {
              List<Integer> path = queue.poll();
              int u = path.get(path.size() - 1);
              if (u == n - 1) {
                  ans.add(path);
                  continue;
              }
              for (int v : graph[u]) {
                  List<Integer> next = new ArrayList<>(path);
                  next.add(v);
                  queue.offer(next);
              }
          }
          return ans;
      }
  }
  
  

• class Solution {
  public:
      vector<vector<int>> graph;
      vector<vector<int>> ans;
  
      vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
          this->graph = graph;
          vector<int> path;
          path.push_back(0);
          dfs(0, path);
          return ans;
      }
  
      void dfs(int i, vector<int> path) {
          if (i == graph.size() - 1) {
              ans.push_back(path);
              return;
          }
          for (int j : graph[i]) {
              path.push_back(j);
              dfs(j, path);
              path.pop_back();
          }
      }
  };
  

• class Solution:
      def allPathsSourceTarget(self, graph: List[List[int]]) -> List[List[int]]:
          n = len(graph)
          q = deque([[0]])
          ans = []
          while q:
              path = q.popleft()
              u = path[-1]
              if u == n - 1:
                  ans.append(path)
                  continue
              for v in graph[u]:
                  q.append(path + [v])
          return ans
  
  

• func allPathsSourceTarget(graph [][]int) [][]int {
  	var path []int
  	path = append(path, 0)
  	var ans [][]int
  
  	var dfs func(i int)
  	dfs = func(i int) {
  		if i == len(graph)-1 {
  			ans = append(ans, append([]int(nil), path...))
  			return
  		}
  		for _, j := range graph[i] {
  			path = append(path, j)
  			dfs(j)
  			path = path[:len(path)-1]
  		}
  	}
  
  	dfs(0)
  	return ans
  }
  

• /**
   * @param {number[][]} graph
   * @return {number[][]}
   */
  var allPathsSourceTarget = function (graph) {
      const ans = [];
      const t = [0];
  
      const dfs = t => {
          const cur = t[t.length - 1];
          if (cur == graph.length - 1) {
              ans.push([...t]);
              return;
          }
          for (const v of graph[cur]) {
              t.push(v);
              dfs(t);
              t.pop();
          }
      };
  
      dfs(t);
      return ans;
  };
  
  

• impl Solution {
      fn dfs(i: usize, path: &mut Vec<i32>, res: &mut Vec<Vec<i32>>, graph: &Vec<Vec<i32>>) {
          path.push(i as i32);
          if i == graph.len() - 1 {
              res.push(path.clone());
          }
          for j in graph[i].iter() {
              Self::dfs(*j as usize, path, res, graph);
          }
          path.pop();
      }
  
      pub fn all_paths_source_target(graph: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
          let mut res = Vec::new();
          Self::dfs(0, &mut vec![], &mut res, &graph);
          res
      }
  }
  
  

• function allPathsSourceTarget(graph: number[][]): number[][] {
      const ans: number[][] = [];
  
      const dfs = (path: number[]) => {
          const curr = path.at(-1)!;
          if (curr === graph.length - 1) {
              ans.push([...path]);
              return;
          }
  
          for (const v of graph[curr]) {
              path.push(v);
              dfs(path);
              path.pop();
          }
      };
  
      dfs([0]);
  
      return ans;
  }
  
  

All Problems

All Solutions