Welcome to Subscribe On Youtube
787. Cheapest Flights Within K Stops
Description
There are n cities connected by some number of flights. You are given an array flights where flights[i] = [fromi, toi, pricei] indicates that there is a flight from city fromi to city toi with cost pricei.
You are also given three integers src, dst, and k, return the cheapest price from src to dst with at most k stops. If there is no such route, return -1.
Example 1:
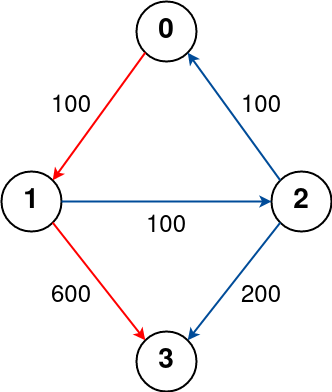
Input: n = 4, flights = [[0,1,100],[1,2,100],[2,0,100],[1,3,600],[2,3,200]], src = 0, dst = 3, k = 1 Output: 700 Explanation: The graph is shown above. The optimal path with at most 1 stop from city 0 to 3 is marked in red and has cost 100 + 600 = 700. Note that the path through cities [0,1,2,3] is cheaper but is invalid because it uses 2 stops.
Example 2:
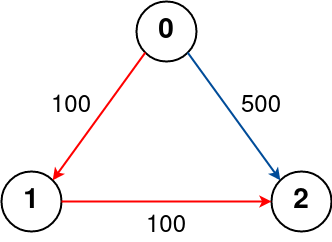
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1 Output: 200 Explanation: The graph is shown above. The optimal path with at most 1 stop from city 0 to 2 is marked in red and has cost 100 + 100 = 200.
Example 3:
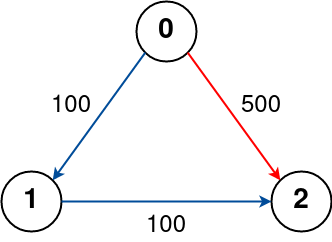
Input: n = 3, flights = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 0 Output: 500 Explanation: The graph is shown above. The optimal path with no stops from city 0 to 2 is marked in red and has cost 500.
Constraints:
1 <= n <= 1000 <= flights.length <= (n * (n - 1) / 2)flights[i].length == 30 <= fromi, toi < nfromi != toi1 <= pricei <= 104- There will not be any multiple flights between two cities.
0 <= src, dst, k < nsrc != dst
Solutions
-
class Solution { private static final int INF = 0x3f3f3f3f; public int findCheapestPrice(int n, int[][] flights, int src, int dst, int k) { int[] dist = new int[n]; int[] backup = new int[n]; Arrays.fill(dist, INF); dist[src] = 0; for (int i = 0; i < k + 1; ++i) { System.arraycopy(dist, 0, backup, 0, n); for (int[] e : flights) { int f = e[0], t = e[1], p = e[2]; dist[t] = Math.min(dist[t], backup[f] + p); } } return dist[dst] == INF ? -1 : dist[dst]; } } -
class Solution { public: int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int k) { const int inf = 0x3f3f3f3f; vector<int> dist(n, inf); vector<int> backup; dist[src] = 0; for (int i = 0; i < k + 1; ++i) { backup = dist; for (auto& e : flights) { int f = e[0], t = e[1], p = e[2]; dist[t] = min(dist[t], backup[f] + p); } } return dist[dst] == inf ? -1 : dist[dst]; } }; -
class Solution: def findCheapestPrice( self, n: int, flights: List[List[int]], src: int, dst: int, k: int ) -> int: INF = 0x3F3F3F3F dist = [INF] * n dist[src] = 0 for _ in range(k + 1): backup = dist.copy() for f, t, p in flights: dist[t] = min(dist[t], backup[f] + p) return -1 if dist[dst] == INF else dist[dst] -
func findCheapestPrice(n int, flights [][]int, src int, dst int, k int) int { const inf = 0x3f3f3f3f dist := make([]int, n) backup := make([]int, n) for i := range dist { dist[i] = inf } dist[src] = 0 for i := 0; i < k+1; i++ { copy(backup, dist) for _, e := range flights { f, t, p := e[0], e[1], e[2] dist[t] = min(dist[t], backup[f]+p) } } if dist[dst] == inf { return -1 } return dist[dst] }