Welcome to Subscribe On Youtube
782. Transform to Chessboard
Description
You are given an n x n binary grid board. In each move, you can swap any two rows with each other, or any two columns with each other.
Return the minimum number of moves to transform the board into a chessboard board. If the task is impossible, return -1.
A chessboard board is a board where no 0's and no 1's are 4-directionally adjacent.
Example 1:
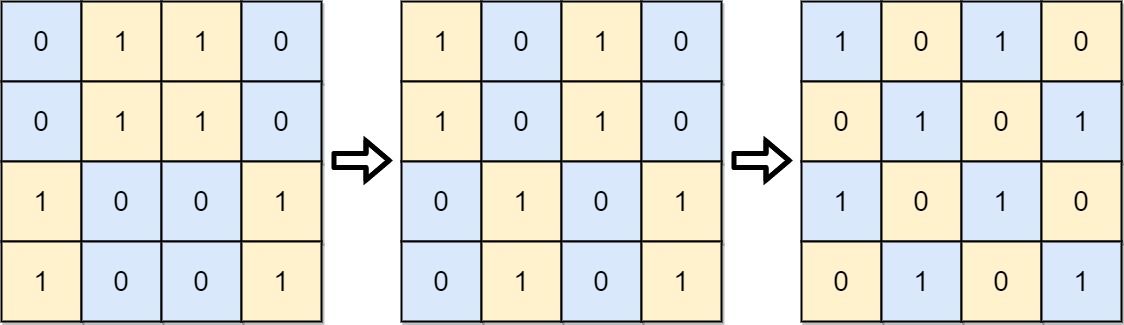
Input: board = [[0,1,1,0],[0,1,1,0],[1,0,0,1],[1,0,0,1]] Output: 2 Explanation: One potential sequence of moves is shown. The first move swaps the first and second column. The second move swaps the second and third row.
Example 2:
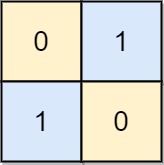
Input: board = [[0,1],[1,0]] Output: 0 Explanation: Also note that the board with 0 in the top left corner, is also a valid chessboard.
Example 3:
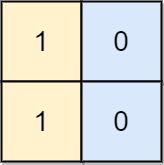
Input: board = [[1,0],[1,0]] Output: -1 Explanation: No matter what sequence of moves you make, you cannot end with a valid chessboard.
Constraints:
n == board.lengthn == board[i].length2 <= n <= 30board[i][j]is either0or1.
Solutions
-
class Solution { private int n; public int movesToChessboard(int[][] board) { n = board.length; int mask = (1 << n) - 1; int rowMask = 0, colMask = 0; for (int i = 0; i < n; ++i) { rowMask |= board[0][i] << i; colMask |= board[i][0] << i; } int revRowMask = mask ^ rowMask; int revColMask = mask ^ colMask; int sameRow = 0, sameCol = 0; for (int i = 0; i < n; ++i) { int curRowMask = 0, curColMask = 0; for (int j = 0; j < n; ++j) { curRowMask |= board[i][j] << j; curColMask |= board[j][i] << j; } if (curRowMask != rowMask && curRowMask != revRowMask) { return -1; } if (curColMask != colMask && curColMask != revColMask) { return -1; } sameRow += curRowMask == rowMask ? 1 : 0; sameCol += curColMask == colMask ? 1 : 0; } int t1 = f(rowMask, sameRow); int t2 = f(colMask, sameCol); return t1 == -1 || t2 == -1 ? -1 : t1 + t2; } private int f(int mask, int cnt) { int ones = Integer.bitCount(mask); if (n % 2 == 1) { if (Math.abs(n - ones * 2) != 1 || Math.abs(n - cnt * 2) != 1) { return -1; } if (ones == n / 2) { return n / 2 - Integer.bitCount(mask & 0xAAAAAAAA); } return (n / 2 + 1) - Integer.bitCount(mask & 0x55555555); } else { if (ones != n / 2 || cnt != n / 2) { return -1; } int cnt0 = n / 2 - Integer.bitCount(mask & 0xAAAAAAAA); int cnt1 = n / 2 - Integer.bitCount(mask & 0x55555555); return Math.min(cnt0, cnt1); } } } -
class Solution { public: int n; int movesToChessboard(vector<vector<int>>& board) { n = board.size(); int mask = (1 << n) - 1; int rowMask = 0, colMask = 0; for (int i = 0; i < n; ++i) { rowMask |= board[0][i] << i; colMask |= board[i][0] << i; } int revRowMask = mask ^ rowMask; int revColMask = mask ^ colMask; int sameRow = 0, sameCol = 0; for (int i = 0; i < n; ++i) { int curRowMask = 0, curColMask = 0; for (int j = 0; j < n; ++j) { curRowMask |= board[i][j] << j; curColMask |= board[j][i] << j; } if (curRowMask != rowMask && curRowMask != revRowMask) return -1; if (curColMask != colMask && curColMask != revColMask) return -1; sameRow += curRowMask == rowMask; sameCol += curColMask == colMask; } int t1 = f(rowMask, sameRow); int t2 = f(colMask, sameCol); return t1 == -1 || t2 == -1 ? -1 : t1 + t2; } int f(int mask, int cnt) { int ones = __builtin_popcount(mask); if (n & 1) { if (abs(n - ones * 2) != 1 || abs(n - cnt * 2) != 1) return -1; if (ones == n / 2) return n / 2 - __builtin_popcount(mask & 0xAAAAAAAA); return (n + 1) / 2 - __builtin_popcount(mask & 0x55555555); } else { if (ones != n / 2 || cnt != n / 2) return -1; int cnt0 = (n / 2 - __builtin_popcount(mask & 0xAAAAAAAA)); int cnt1 = (n / 2 - __builtin_popcount(mask & 0x55555555)); return min(cnt0, cnt1); } } }; -
class Solution: def movesToChessboard(self, board: List[List[int]]) -> int: def f(mask, cnt): ones = mask.bit_count() if n & 1: if abs(n - 2 * ones) != 1 or abs(n - 2 * cnt) != 1: return -1 if ones == n // 2: return n // 2 - (mask & 0xAAAAAAAA).bit_count() return (n + 1) // 2 - (mask & 0x55555555).bit_count() else: if ones != n // 2 or cnt != n // 2: return -1 cnt0 = n // 2 - (mask & 0xAAAAAAAA).bit_count() cnt1 = n // 2 - (mask & 0x55555555).bit_count() return min(cnt0, cnt1) n = len(board) mask = (1 << n) - 1 rowMask = colMask = 0 for i in range(n): rowMask |= board[0][i] << i colMask |= board[i][0] << i revRowMask = mask ^ rowMask revColMask = mask ^ colMask sameRow = sameCol = 0 for i in range(n): curRowMask = curColMask = 0 for j in range(n): curRowMask |= board[i][j] << j curColMask |= board[j][i] << j if curRowMask not in (rowMask, revRowMask) or curColMask not in ( colMask, revColMask, ): return -1 sameRow += curRowMask == rowMask sameCol += curColMask == colMask t1 = f(rowMask, sameRow) t2 = f(colMask, sameCol) return -1 if t1 == -1 or t2 == -1 else t1 + t2 -
func movesToChessboard(board [][]int) int { n := len(board) mask := (1 << n) - 1 rowMask, colMask := 0, 0 for i := 0; i < n; i++ { rowMask |= board[0][i] << i colMask |= board[i][0] << i } revRowMask := mask ^ rowMask revColMask := mask ^ colMask sameRow, sameCol := 0, 0 for i := 0; i < n; i++ { curRowMask, curColMask := 0, 0 for j := 0; j < n; j++ { curRowMask |= board[i][j] << j curColMask |= board[j][i] << j } if curRowMask != rowMask && curRowMask != revRowMask { return -1 } if curColMask != colMask && curColMask != revColMask { return -1 } if curRowMask == rowMask { sameRow++ } if curColMask == colMask { sameCol++ } } f := func(mask, cnt int) int { ones := bits.OnesCount(uint(mask)) if n%2 == 1 { if abs(n-ones*2) != 1 || abs(n-cnt*2) != 1 { return -1 } if ones == n/2 { return n/2 - bits.OnesCount(uint(mask&0xAAAAAAAA)) } return (n+1)/2 - bits.OnesCount(uint(mask&0x55555555)) } else { if ones != n/2 || cnt != n/2 { return -1 } cnt0 := n/2 - bits.OnesCount(uint(mask&0xAAAAAAAA)) cnt1 := n/2 - bits.OnesCount(uint(mask&0x55555555)) return min(cnt0, cnt1) } } t1 := f(rowMask, sameRow) t2 := f(colMask, sameCol) if t1 == -1 || t2 == -1 { return -1 } return t1 + t2 } func abs(x int) int { if x < 0 { return -x } return x }