Welcome to Subscribe On Youtube

743. Network Delay Time

Description

You are given a network of n nodes, labeled from 1 to n. You are also given times, a list of travel times as directed edges times[i] = (ui, vi, wi), where ui is the source node, vi is the target node, and wi is the time it takes for a signal to travel from source to target.

We will send a signal from a given node k. Return the minimum time it takes for all the n nodes to receive the signal. If it is impossible for all the n nodes to receive the signal, return -1.

 

Example 1:

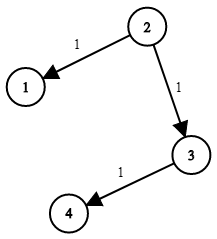
Input: times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
Output: 2

Example 2:

Input: times = [[1,2,1]], n = 2, k = 1
Output: 1

Example 3:

Input: times = [[1,2,1]], n = 2, k = 2
Output: -1

 

Constraints:

• 1 <= k <= n <= 100
• 1 <= times.length <= 6000
• times[i].length == 3
• 1 <= ui, vi <= n
• ui != vi
• 0 <= wi <= 100
• All the pairs (ui, vi) are unique. (i.e., no multiple edges.)

Solutions

• Java
• C++
• Python
• Go
• TypeScript

• class Solution {
      private static final int N = 110;
      private static final int INF = 0x3f3f;
  
      public int networkDelayTime(int[][] times, int n, int k) {
          int[][] g = new int[N][N];
          for (int i = 0; i < N; ++i) {
              Arrays.fill(g[i], INF);
          }
          for (int[] e : times) {
              g[e[0]][e[1]] = e[2];
          }
          int[] dist = new int[N];
          Arrays.fill(dist, INF);
          dist[k] = 0;
          boolean[] vis = new boolean[N];
          for (int i = 0; i < n; ++i) {
              int t = -1;
              for (int j = 1; j <= n; ++j) {
                  if (!vis[j] && (t == -1 || dist[t] > dist[j])) {
                      t = j;
                  }
              }
              vis[t] = true;
              for (int j = 1; j <= n; ++j) {
                  dist[j] = Math.min(dist[j], dist[t] + g[t][j]);
              }
          }
          int ans = 0;
          for (int i = 1; i <= n; ++i) {
              ans = Math.max(ans, dist[i]);
          }
          return ans == INF ? -1 : ans;
      }
  }
  

• class Solution {
  public:
      const int inf = 0x3f3f;
  
      int networkDelayTime(vector<vector<int>>& times, int n, int k) {
          vector<vector<int>> g(n, vector<int>(n, inf));
          for (auto& t : times) g[t[0] - 1][t[1] - 1] = t[2];
          vector<bool> vis(n);
          vector<int> dist(n, inf);
          dist[k - 1] = 0;
          for (int i = 0; i < n; ++i) {
              int t = -1;
              for (int j = 0; j < n; ++j) {
                  if (!vis[j] && (t == -1 || dist[t] > dist[j])) {
                      t = j;
                  }
              }
              vis[t] = true;
              for (int j = 0; j < n; ++j) {
                  dist[j] = min(dist[j], dist[t] + g[t][j]);
              }
          }
          int ans = *max_element(dist.begin(), dist.end());
          return ans == inf ? -1 : ans;
      }
  };
  

• class Solution:
      def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
          INF = 0x3F3F
          g = defaultdict(list)
          for u, v, w in times:
              g[u - 1].append((v - 1, w))
          dist = [INF] * n
          dist[k - 1] = 0
          q = [(0, k - 1)]
          while q:
              _, u = heappop(q)
              for v, w in g[u]:
                  if dist[v] > dist[u] + w:
                      dist[v] = dist[u] + w
                      heappush(q, (dist[v], v))
          ans = max(dist)
          return -1 if ans == INF else ans
  
  

• const Inf = 0x3f3f3f3f
  
  type pair struct {
  	first  int
  	second int
  }
  
  var _ heap.Interface = (*pairs)(nil)
  
  type pairs []pair
  
  func (a pairs) Len() int { return len(a) }
  func (a pairs) Less(i int, j int) bool {
  	return a[i].first < a[j].first || a[i].first == a[j].first && a[i].second < a[j].second
  }
  func (a pairs) Swap(i int, j int) { a[i], a[j] = a[j], a[i] }
  func (a *pairs) Push(x any)       { *a = append(*a, x.(pair)) }
  func (a *pairs) Pop() any         { l := len(*a); t := (*a)[l-1]; *a = (*a)[:l-1]; return t }
  
  func networkDelayTime(times [][]int, n int, k int) int {
  	graph := make([]pairs, n)
  	for _, time := range times {
  		from, to, time := time[0]-1, time[1]-1, time[2]
  		graph[from] = append(graph[from], pair{to, time})
  	}
  
  	dis := make([]int, n)
  	for i := range dis {
  		dis[i] = Inf
  	}
  	dis[k-1] = 0
  
  	vis := make([]bool, n)
  	h := make(pairs, 0)
  	heap.Push(&h, pair{0, k - 1})
  	for len(h) > 0 {
  		from := heap.Pop(&h).(pair).second
  		if vis[from] {
  			continue
  		}
  		vis[from] = true
  		for _, e := range graph[from] {
  			to, d := e.first, dis[from]+e.second
  			if d < dis[to] {
  				dis[to] = d
  				heap.Push(&h, pair{d, to})
  			}
  		}
  	}
  	ans := slices.Max(dis)
  	if ans == Inf {
  		return -1
  	}
  	return ans
  }
  

• function networkDelayTime(times: number[][], n: number, k: number): number {
      const g: number[][] = Array.from({ length: n }, () => Array(n).fill(Infinity));
      for (const [u, v, w] of times) {
          g[u - 1][v - 1] = w;
      }
      const dist: number[] = Array(n).fill(Infinity);
      dist[k - 1] = 0;
      const vis: boolean[] = Array(n).fill(false);
      for (let i = 0; i < n; ++i) {
          let t = -1;
          for (let j = 0; j < n; ++j) {
              if (!vis[j] && (t === -1 || dist[j] < dist[t])) {
                  t = j;
              }
          }
          vis[t] = true;
          for (let j = 0; j < n; ++j) {
              dist[j] = Math.min(dist[j], dist[t] + g[t][j]);
          }
      }
      const ans = Math.max(...dist);
      return ans === Infinity ? -1 : ans;
  }
  
  

All Problems

All Solutions