Welcome to Subscribe On Youtube

666. Path Sum IV

Description

If the depth of a tree is smaller than 5, then this tree can be represented by an array of three-digit integers. For each integer in this array:

• The hundreds digit represents the depth d of this node where 1 <= d <= 4.
• The tens digit represents the position p of this node in the level it belongs to where 1 <= p <= 8. The position is the same as that in a full binary tree.
• The units digit represents the value v of this node where 0 <= v <= 9.

Given an array of ascending three-digit integers nums representing a binary tree with a depth smaller than 5, return the sum of all paths from the root towards the leaves.

It is guaranteed that the given array represents a valid connected binary tree.

 

Example 1:

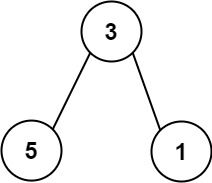
Input: nums = [113,215,221]
Output: 12
Explanation: The tree that the list represents is shown.
The path sum is (3 + 5) + (3 + 1) = 12.

Example 2:

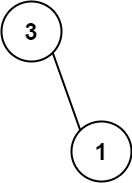
Input: nums = [113,221]
Output: 4
Explanation: The tree that the list represents is shown. 
The path sum is (3 + 1) = 4.

 

Constraints:

• 1 <= nums.length <= 15
• 110 <= nums[i] <= 489
• nums represents a valid binary tree with depth less than 5.

Solutions

DFS.

• Java
• C++
• Python
• Go

• class Solution {
      private int ans;
      private Map<Integer, Integer> mp;
  
      public int pathSum(int[] nums) {
          ans = 0;
          mp = new HashMap<>(nums.length);
          for (int num : nums) {
              mp.put(num / 10, num % 10);
          }
          dfs(11, 0);
          return ans;
      }
  
      private void dfs(int node, int t) {
          if (!mp.containsKey(node)) {
              return;
          }
          t += mp.get(node);
          int d = node / 10, p = node % 10;
          int l = (d + 1) * 10 + (p * 2) - 1;
          int r = l + 1;
          if (!mp.containsKey(l) && !mp.containsKey(r)) {
              ans += t;
              return;
          }
          dfs(l, t);
          dfs(r, t);
      }
  }
  

• class Solution {
  public:
      int ans;
      unordered_map<int, int> mp;
  
      int pathSum(vector<int>& nums) {
          ans = 0;
          mp.clear();
          for (int num : nums) mp[num / 10] = num % 10;
          dfs(11, 0);
          return ans;
      }
  
      void dfs(int node, int t) {
          if (!mp.count(node)) return;
          t += mp[node];
          int d = node / 10, p = node % 10;
          int l = (d + 1) * 10 + (p * 2) - 1;
          int r = l + 1;
          if (!mp.count(l) && !mp.count(r)) {
              ans += t;
              return;
          }
          dfs(l, t);
          dfs(r, t);
      }
  };
  

• class Solution:
      def pathSum(self, nums: List[int]) -> int:
          def dfs(node, t):
              if node not in mp:
                  return
              t += mp[node]
              d, p = divmod(node, 10)
              l = (d + 1) * 10 + (p * 2) - 1
              r = l + 1
              nonlocal ans
              if l not in mp and r not in mp:
                  ans += t
                  return
              dfs(l, t)
              dfs(r, t)
  
          ans = 0
          mp = {num // 10: num % 10 for num in nums}
          dfs(11, 0)
          return ans
  
  

• func pathSum(nums []int) int {
  	ans := 0
  	mp := make(map[int]int)
  	for _, num := range nums {
  		mp[num/10] = num % 10
  	}
  	var dfs func(node, t int)
  	dfs = func(node, t int) {
  		if v, ok := mp[node]; ok {
  			t += v
  			d, p := node/10, node%10
  			l := (d+1)*10 + (p * 2) - 1
  			r := l + 1
  			if _, ok1 := mp[l]; !ok1 {
  				if _, ok2 := mp[r]; !ok2 {
  					ans += t
  					return
  				}
  			}
  			dfs(l, t)
  			dfs(r, t)
  		}
  	}
  	dfs(11, 0)
  	return ans
  }
  

All Problems

All Solutions