Welcome to Subscribe On Youtube
654. Maximum Binary Tree
Description
You are given an integer array nums with no duplicates. A maximum binary tree can be built recursively from nums using the following algorithm:
- Create a root node whose value is the maximum value in
nums. - Recursively build the left subtree on the subarray prefix to the left of the maximum value.
- Recursively build the right subtree on the subarray suffix to the right of the maximum value.
Return the maximum binary tree built from nums.
Example 1:
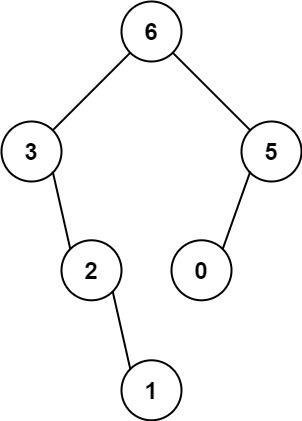
Input: nums = [3,2,1,6,0,5]
Output: [6,3,5,null,2,0,null,null,1]
Explanation: The recursive calls are as follow:
- The largest value in [3,2,1,6,0,5] is 6. Left prefix is [3,2,1] and right suffix is [0,5].
- The largest value in [3,2,1] is 3. Left prefix is [] and right suffix is [2,1].
- Empty array, so no child.
- The largest value in [2,1] is 2. Left prefix is [] and right suffix is [1].
- Empty array, so no child.
- Only one element, so child is a node with value 1.
- The largest value in [0,5] is 5. Left prefix is [0] and right suffix is [].
- Only one element, so child is a node with value 0.
- Empty array, so no child.
Example 2:
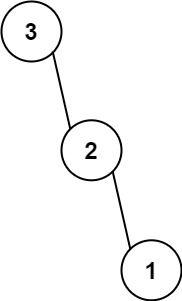
Input: nums = [3,2,1] Output: [3,null,2,null,1]
Constraints:
1 <= nums.length <= 10000 <= nums[i] <= 1000- All integers in
numsare unique.
Solutions
-
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { private int[] nums; public TreeNode constructMaximumBinaryTree(int[] nums) { this.nums = nums; return dfs(0, nums.length - 1); } private TreeNode dfs(int l, int r) { if (l > r) { return null; } int i = l; for (int j = l; j <= r; ++j) { if (nums[i] < nums[j]) { i = j; } } TreeNode root = new TreeNode(nums[i]); root.left = dfs(l, i - 1); root.right = dfs(i + 1, r); return root; } } -
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: TreeNode* constructMaximumBinaryTree(vector<int>& nums) { return dfs(nums, 0, nums.size() - 1); } TreeNode* dfs(vector<int>& nums, int l, int r) { if (l > r) return nullptr; int i = l; for (int j = l; j <= r; ++j) { if (nums[i] < nums[j]) { i = j; } } TreeNode* root = new TreeNode(nums[i]); root->left = dfs(nums, l, i - 1); root->right = dfs(nums, i + 1, r); return root; } }; -
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]: def dfs(nums): if not nums: return None val = max(nums) i = nums.index(val) root = TreeNode(val) root.left = dfs(nums[:i]) root.right = dfs(nums[i + 1 :]) return root return dfs(nums) -
/** * Definition for a binary tree node. * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */ func constructMaximumBinaryTree(nums []int) *TreeNode { var dfs func(l, r int) *TreeNode dfs = func(l, r int) *TreeNode { if l > r { return nil } i := l for j := l; j <= r; j++ { if nums[i] < nums[j] { i = j } } root := &TreeNode{Val: nums[i]} root.Left = dfs(l, i-1) root.Right = dfs(i+1, r) return root } return dfs(0, len(nums)-1) } -
/** * Definition for a binary tree node. * class TreeNode { * val: number * left: TreeNode | null * right: TreeNode | null * constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } * } */ function constructMaximumBinaryTree(nums: number[]): TreeNode | null { const n = nums.length; if (n === 0) { return null; } const [val, i] = nums.reduce((r, v, i) => (r[0] < v ? [v, i] : r), [-1, 0]); return new TreeNode( val, constructMaximumBinaryTree(nums.slice(0, i)), constructMaximumBinaryTree(nums.slice(i + 1)), ); } -
// Definition for a binary tree node. // #[derive(Debug, PartialEq, Eq)] // pub struct TreeNode { // pub val: i32, // pub left: Option<Rc<RefCell<TreeNode>>>, // pub right: Option<Rc<RefCell<TreeNode>>>, // } // // impl TreeNode { // #[inline] // pub fn new(val: i32) -> Self { // TreeNode { // val, // left: None, // right: None // } // } // } use std::rc::Rc; use std::cell::RefCell; impl Solution { fn construct(nums: &Vec<i32>, start: usize, end: usize) -> Option<Rc<RefCell<TreeNode>>> { if start >= end { return None; } let mut idx = 0; let mut max_val = -1; for i in start..end { if nums[i] > max_val { idx = i; max_val = nums[i]; } } Some( Rc::new( RefCell::new(TreeNode { val: max_val, left: Self::construct(nums, start, idx), right: Self::construct(nums, idx + 1, end), }) ) ) } pub fn construct_maximum_binary_tree(nums: Vec<i32>) -> Option<Rc<RefCell<TreeNode>>> { Self::construct(&nums, 0, nums.len()) } }