653. Two Sum IV - Input is a BST

Description

Given the root of a binary search tree and an integer k, return true if there exist two elements in the BST such that their sum is equal to k, or false otherwise.

Example 1:

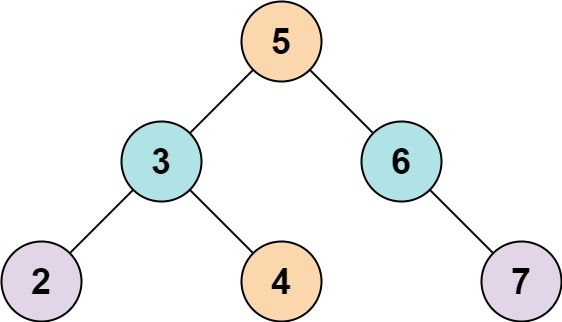
Input: root = [5,3,6,2,4,null,7], k = 9
Output: true

Example 2:

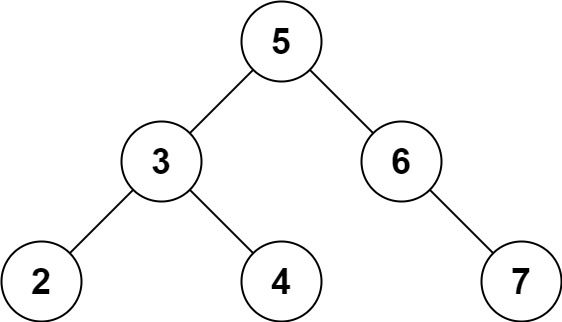
Input: root = [5,3,6,2,4,null,7], k = 28
Output: false

Constraints:

The number of nodes in the tree is in the range [1, 10⁴].
-10⁴ <= Node.val <= 10⁴
root is guaranteed to be a valid binary search tree.
-10⁵ <= k <= 10⁵

Solution 1 - set

As long as it is the question of the sum of two numbers, you must remember to try to do it with HashSet.

This question is just to turn the array into a binary tree. We need to traverse the binary tree and use a HashSet. In the recursive function function,

if node is empty, return false.
If k minus the current node value exists in the HashSet, return true directly;
otherwise, add the current node value to the HashSet, and then call the recursive function on the left and right sub-nodes and return together.

Solution 2 - two pointers

This solution defines two classes: BSTIterator and Solution. The BSTIterator class is designed to iterate through a binary search tree (BST) in either ascending (left-to-right) or descending (right-to-left) order. The Solution class uses two instances of BSTIterator to find if there exists two elements in the BST such that their sum equals a given target value k.

Class: `BSTIterator`

Constructor __init__: Initializes the iterator with the root of a BST and a boolean flag leftToRight indicating the direction of iteration (ascending if True, descending if False). It initializes an empty stack to facilitate controlled traversal of the BST and calls _pushUntilNone to preload the stack with the initial path from the root towards the leftmost or rightmost node, depending on the iteration direction.
Method next: Returns the next integer in the sequence. It pops the top element from the stack (which is the next element in order), then, depending on the iteration direction, traverses towards the next node in that order, pushing nodes encountered along the way onto the stack. This ensures that the stack always contains the nodes that maintain the current path in the tree relevant to the iteration order.
Method _pushUntilNone: Given a starting node, it iteratively traverses the tree towards the leftmost (for ascending order) or rightmost (for descending order) node, pushing all encountered nodes onto the stack. This method ensures that the next call to next will return the next correct value in the sequence.

Class: `Solution`

Method findTarget: This method checks if there are two numbers in the BST that add up to k. It initializes two BSTIterator instances, one for ascending order (left) and one for descending order (right). It then iterates through the BST from both ends simultaneously (smallest and largest values), comparing their sum to k.
- If the sum equals k, it returns True.
- If the sum is less than k, it moves the left iterator to the next larger value.
- If the sum is greater than k, it moves the right iterator to the next smaller value.
- This process continues until the left value is no longer less than the right value, meaning the entire BST has been examined.

By approaching from both the smallest and largest values simultaneously and narrowing down the search space based on the sum comparison, this method efficiently determines whether any two elements in the BST add up to k.

Example Scenario

Consider a BST with elements [2, 3, 4, 5, 6, 7] and a target sum k = 9.

The left iterator starts at 2 (the smallest value), and the right iterator starts at 7 (the largest value).
Since their sum 2 + 7 = 9 equals k, the method immediately returns True.

This approach effectively leverages the BST property (left child < parent < right child) and two-pointer technique to find the target sum with optimal efficiency.

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
public class Two_Sum_IV_Input_is_a_BST {
    /**
     * Definition for a binary tree node.
     * public class TreeNode {
     *     int val;
     *     TreeNode left;
     *     TreeNode right;
     *     TreeNode(int x) { val = x; }
     * }
     */

    // https://leetcode.com/problems/two-sum-iv-input-is-a-bst/solution/
    public class Solution_queue {
        public boolean findTarget(TreeNode root, int k) {
            Set<Integer> set = new HashSet<>();
            Queue<TreeNode> queue = new LinkedList<>();
            queue.add(root);
            while (!queue.isEmpty()) {
                if (queue.peek() != null) {
                    TreeNode node = queue.remove();
                    if (set.contains(k - node.val))
                        return true;
                    set.add(node.val);
                    queue.add(node.right);
                    queue.add(node.left);
                } else
                    queue.remove();
            }
            return false;
        }
    }

    // time: O(N)
    // space: O(N)
    public class Solution_usingBST { // inorder traversal to get sorted list
        public boolean findTarget(TreeNode root, int k) {
            List< Integer > list = new ArrayList<>();
            inorder(root, list);
            int l = 0, r = list.size() - 1;
            while (l < r) {
                int sum = list.get(l) + list.get(r);
                if (sum == k)
                    return true;
                if (sum < k)
                    l++;
                else
                    r--;
            }
            return false;
        }
        public void inorder(TreeNode root, List < Integer > list) {
            if (root == null)
                return;
            inorder(root.left, list);
            list.add(root.val);
            inorder(root.right, list);
        }
    }

    // time: O(N)
    // space: O(N)
    public class Solution {
        public boolean findTarget(TreeNode root, int k) {
            Set < Integer > set = new HashSet();
            return find(root, k, set);
        }

        public boolean find(TreeNode root, int k, Set< Integer > set) {
            if (root == null) {
                return false;
            }
            if (set.contains(k - root.val)) {
                return true;
            }
            set.add(root.val);

            return find(root.left, k, set) || find(root.right, k, set);
        }
    }

}

//////

class Solution {
    private Set<Integer> vis = new HashSet<>();
    private int k;

    public boolean findTarget(TreeNode root, int k) {
        this.k = k;
        return dfs(root);
    }

    private boolean dfs(TreeNode root) {
        if (root == null) {
            return false;
        }
        if (vis.contains(k - root.val)) {
            return true;
        }
        vis.add(root.val);
        return dfs(root.left) || dfs(root.right);
    }
}

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool findTarget(TreeNode* root, int k) {
        unordered_set<int> vis;

        function<bool(TreeNode*)> dfs = [&](TreeNode* root) {
            if (!root) {
                return false;
            }
            if (vis.count(k - root->val)) {
                return true;
            }
            vis.insert(root->val);
            return dfs(root->left) || dfs(root->right);
        };
        return dfs(root);
    }
};

class BSTIterator:
    def __init__(self, root: Optional[TreeNode], leftToRight: bool):
        self.stack = []
        self.leftToRight = leftToRight
        self._pushUntilNone(root)

    def next(self) -> int:
        node = self.stack.pop()
        if self.leftToRight:
            self._pushUntilNone(node.right)
        else:
            self._pushUntilNone(node.left)
        return node.val

    # if passed in a None node, then None will not be pushed to stack
    def _pushUntilNone(self, root: Optional[TreeNode]):
        while root:
            self.stack.append(root)
            root = root.left if self.leftToRight else root.right


class Solution:
    def findTarget(self, root: Optional[TreeNode], k: int) -> bool:
        if not root:
            return False

        left = BSTIterator(root, True)
        right = BSTIterator(root, False)

        l = left.next()
        r = right.next()
        while l < r:
            summ = l + r
            if summ == k:
                return True
            if summ < k:
                l = left.next()
            else:
                r = right.next()

        return False

###########

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def findTarget(self, root: Optional[TreeNode], k: int) -> bool:
        def dfs(root):
            if root is None:
                return False
            if k - root.val in vis:
                return True
            vis.add(root.val)
            return dfs(root.left) or dfs(root.right)

        vis = set()
        return dfs(root)

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func findTarget(root *TreeNode, k int) bool {
	vis := map[int]bool{}
	var dfs func(*TreeNode) bool
	dfs = func(root *TreeNode) bool {
		if root == nil {
			return false
		}
		if vis[k-root.Val] {
			return true
		}
		vis[root.Val] = true
		return dfs(root.Left) || dfs(root.Right)
	}
	return dfs(root)
}

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function findTarget(root: TreeNode | null, k: number): boolean {
    const dfs = (root: TreeNode | null) => {
        if (!root) {
            return false;
        }
        if (vis.has(k - root.val)) {
            return true;
        }
        vis.add(root.val);
        return dfs(root.left) || dfs(root.right);
    };
    const vis = new Set<number>();
    return dfs(root);
}

// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
use std::cell::RefCell;
use std::collections::{ HashSet, VecDeque };
use std::rc::Rc;
impl Solution {
    pub fn find_target(root: Option<Rc<RefCell<TreeNode>>>, k: i32) -> bool {
        let mut set = HashSet::new();
        let mut q = VecDeque::new();
        q.push_back(root);
        while let Some(node) = q.pop_front() {
            if let Some(node) = node {
                let mut node = node.as_ref().borrow_mut();
                if set.contains(&node.val) {
                    return true;
                }
                set.insert(k - node.val);
                q.push_back(node.left.take());
                q.push_back(node.right.take());
            }
        }
        false
    }
}

653 - Two Sum IV - Input is a BST

653. Two Sum IV - Input is a BST

Description

Solution 1 - set

Solution 2 - two pointers

Class: `BSTIterator`

Class: `Solution`

Example Scenario

All Problems

All Solutions

Welcome to Subscribe On Youtube

653. Two Sum IV - Input is a BST

Description

Solution 1 - set

Solution 2 - two pointers

Class: BSTIterator

Class: Solution

Example Scenario

All Problems

All Solutions

Class: `BSTIterator`

Class: `Solution`