Welcome to Subscribe On Youtube
623. Add One Row to Tree
Description
Given the root of a binary tree and two integers val and depth, add a row of nodes with value val at the given depth depth.
Note that the root node is at depth 1.
The adding rule is:
- Given the integer
depth, for each not null tree nodecurat the depthdepth - 1, create two tree nodes with valuevalascur's left subtree root and right subtree root. cur's original left subtree should be the left subtree of the new left subtree root.cur's original right subtree should be the right subtree of the new right subtree root.- If
depth == 1that means there is no depthdepth - 1at all, then create a tree node with valuevalas the new root of the whole original tree, and the original tree is the new root's left subtree.
Example 1:
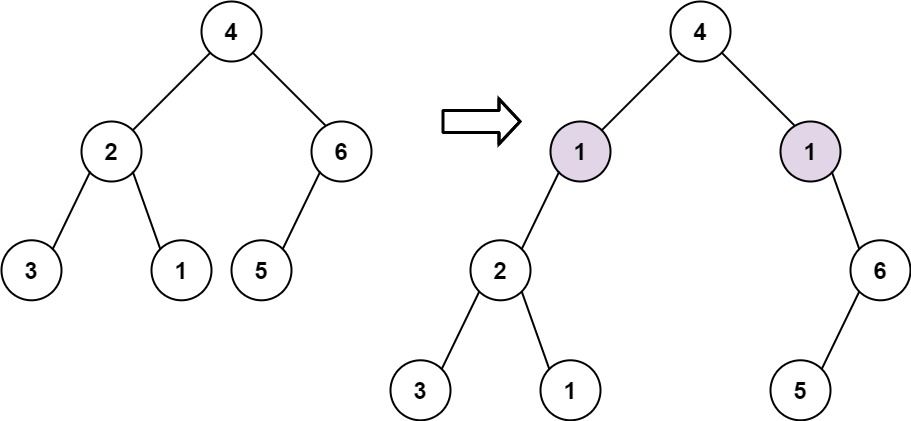
Input: root = [4,2,6,3,1,5], val = 1, depth = 2 Output: [4,1,1,2,null,null,6,3,1,5]
Example 2:
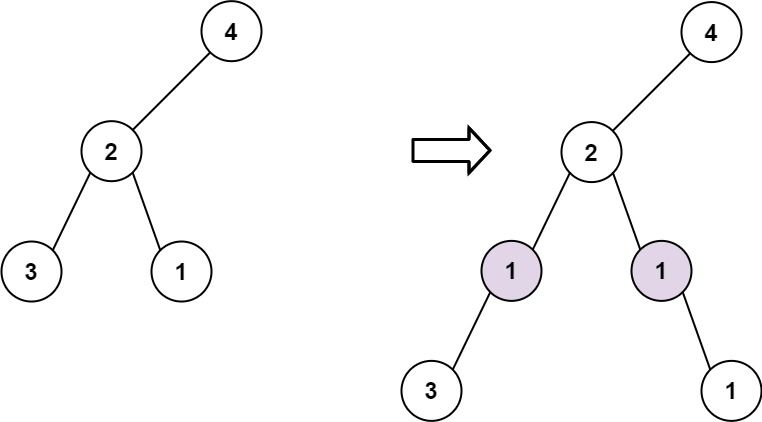
Input: root = [4,2,null,3,1], val = 1, depth = 3 Output: [4,2,null,1,1,3,null,null,1]
Constraints:
- The number of nodes in the tree is in the range
[1, 104]. - The depth of the tree is in the range
[1, 104]. -100 <= Node.val <= 100-105 <= val <= 1051 <= depth <= the depth of tree + 1
Solutions
-
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { private int val; private int depth; public TreeNode addOneRow(TreeNode root, int val, int depth) { if (depth == 1) { return new TreeNode(val, root, null); } this.val = val; this.depth = depth; dfs(root, 1); return root; } private void dfs(TreeNode root, int d) { if (root == null) { return; } if (d == depth - 1) { TreeNode l = new TreeNode(val, root.left, null); TreeNode r = new TreeNode(val, null, root.right); root.left = l; root.right = r; return; } dfs(root.left, d + 1); dfs(root.right, d + 1); } } -
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: int val; int depth; TreeNode* addOneRow(TreeNode* root, int val, int depth) { if (depth == 1) return new TreeNode(val, root, nullptr); this->val = val; this->depth = depth; dfs(root, 1); return root; } void dfs(TreeNode* root, int d) { if (!root) return; if (d == depth - 1) { auto l = new TreeNode(val, root->left, nullptr); auto r = new TreeNode(val, nullptr, root->right); root->left = l; root->right = r; return; } dfs(root->left, d + 1); dfs(root->right, d + 1); } }; -
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def addOneRow( self, root: Optional[TreeNode], val: int, depth: int ) -> Optional[TreeNode]: def dfs(root, d): if root is None: return if d == depth - 1: root.left = TreeNode(val, root.left, None) root.right = TreeNode(val, None, root.right) return dfs(root.left, d + 1) dfs(root.right, d + 1) if depth == 1: return TreeNode(val, root) dfs(root, 1) return root -
/** * Definition for a binary tree node. * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */ func addOneRow(root *TreeNode, val int, depth int) *TreeNode { if depth == 1 { return &TreeNode{Val: val, Left: root} } var dfs func(root *TreeNode, d int) dfs = func(root *TreeNode, d int) { if root == nil { return } if d == depth-1 { l, r := &TreeNode{Val: val, Left: root.Left}, &TreeNode{Val: val, Right: root.Right} root.Left, root.Right = l, r return } dfs(root.Left, d+1) dfs(root.Right, d+1) } dfs(root, 1) return root } -
/** * Definition for a binary tree node. * class TreeNode { * val: number * left: TreeNode | null * right: TreeNode | null * constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } * } */ function addOneRow(root: TreeNode | null, val: number, depth: number): TreeNode | null { if (depth === 1) { return new TreeNode(val, root); } const queue = [root]; for (let i = 1; i < depth - 1; i++) { const n = queue.length; for (let j = 0; j < n; j++) { const { left, right } = queue.shift(); left && queue.push(left); right && queue.push(right); } } for (const node of queue) { node.left = new TreeNode(val, node.left); node.right = new TreeNode(val, null, node.right); } return root; }