Welcome to Subscribe On Youtube

559. Maximum Depth of N-ary Tree

Description

Given a n-ary tree, find its maximum depth.

The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples).

 

Example 1:

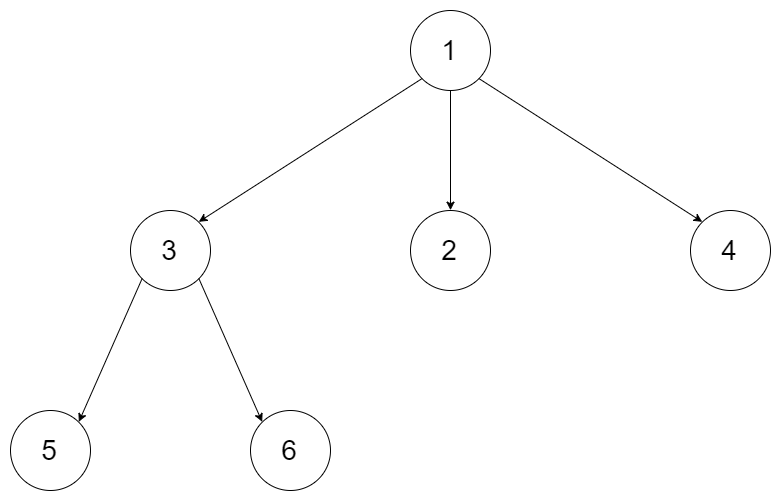
Input: root = [1,null,3,2,4,null,5,6]
Output: 3

Example 2:

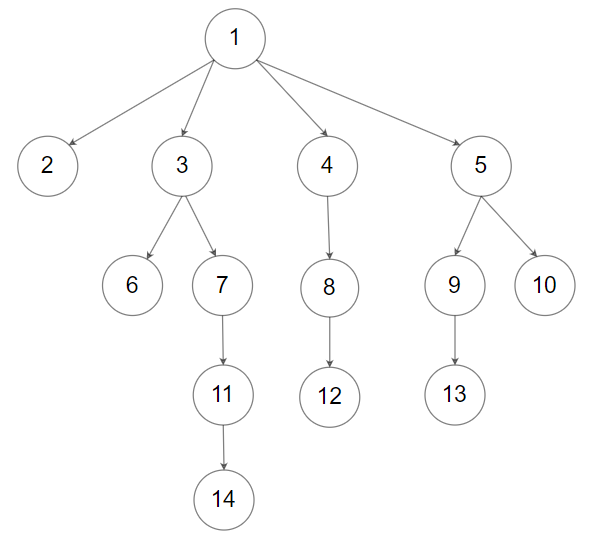
Input: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
Output: 5

 

Constraints:

• The total number of nodes is in the range [0, 104].
• The depth of the n-ary tree is less than or equal to 1000.

Solutions

• Java
• C++
• Python
• Go

• /*
  // Definition for a Node.
  class Node {
      public int val;
      public List<Node> children;
  
      public Node() {}
  
      public Node(int _val) {
          val = _val;
      }
  
      public Node(int _val, List<Node> _children) {
          val = _val;
          children = _children;
      }
  };
  */
  
  class Solution {
      public int maxDepth(Node root) {
          if (root == null) {
              return 0;
          }
          int ans = 1;
          for (Node child : root.children) {
              ans = Math.max(ans, 1 + maxDepth(child));
          }
          return ans;
      }
  }
  

• /*
  // Definition for a Node.
  class Node {
  public:
      int val;
      vector<Node*> children;
  
      Node() {}
  
      Node(int _val) {
          val = _val;
      }
  
      Node(int _val, vector<Node*> _children) {
          val = _val;
          children = _children;
      }
  };
  */
  
  class Solution {
  public:
      int maxDepth(Node* root) {
          if (!root) return 0;
          int ans = 1;
          for (auto& child : root->children) ans = max(ans, 1 + maxDepth(child));
          return ans;
      }
  };
  

• """
  # Definition for a Node.
  class Node:
      def __init__(self, val=None, children=None):
          self.val = val
          self.children = children
  """
  
  
  class Solution:
      def maxDepth(self, root: 'Node') -> int:
          if root is None:
              return 0
          return 1 + max([self.maxDepth(child) for child in root.children], default=0)
  
  

• /**
   * Definition for a Node.
   * type Node struct {
   *     Val int
   *     Children []*Node
   * }
   */
  
  func maxDepth(root *Node) int {
  	if root == nil {
  		return 0
  	}
  	ans := 1
  	for _, child := range root.Children {
  		ans = max(ans, 1+maxDepth(child))
  	}
  	return ans
  }
  

All Problems

All Solutions