Welcome to Subscribe On Youtube
558. Logical OR of Two Binary Grids Represented as Quad-Trees
Description
A Binary Matrix is a matrix in which all the elements are either 0 or 1.
Given quadTree1 and quadTree2. quadTree1 represents a n * n binary matrix and quadTree2 represents another n * n binary matrix.
Return a Quad-Tree representing the n * n binary matrix which is the result of logical bitwise OR of the two binary matrixes represented by quadTree1 and quadTree2.
Notice that you can assign the value of a node to True or False when isLeaf is False, and both are accepted in the answer.
A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:
val: True if the node represents a grid of 1's or False if the node represents a grid of 0's.isLeaf: True if the node is leaf node on the tree or False if the node has the four children.
class Node {
public boolean val;
public boolean isLeaf;
public Node topLeft;
public Node topRight;
public Node bottomLeft;
public Node bottomRight;
}
We can construct a Quad-Tree from a two-dimensional area using the following steps:
- If the current grid has the same value (i.e all
1'sor all0's) setisLeafTrue and setvalto the value of the grid and set the four children to Null and stop. - If the current grid has different values, set
isLeafto False and setvalto any value and divide the current grid into four sub-grids as shown in the photo. - Recurse for each of the children with the proper sub-grid.
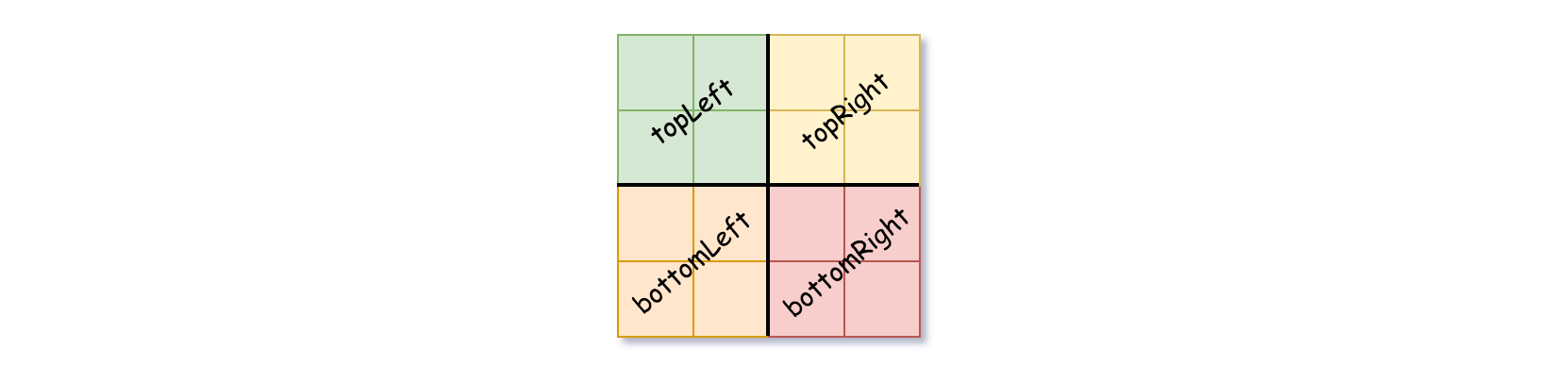
If you want to know more about the Quad-Tree, you can refer to the wiki.
Quad-Tree format:
The input/output represents the serialized format of a Quad-Tree using level order traversal, where null signifies a path terminator where no node exists below.
It is very similar to the serialization of the binary tree. The only difference is that the node is represented as a list [isLeaf, val].
If the value of isLeaf or val is True we represent it as 1 in the list [isLeaf, val] and if the value of isLeaf or val is False we represent it as 0.
Example 1:
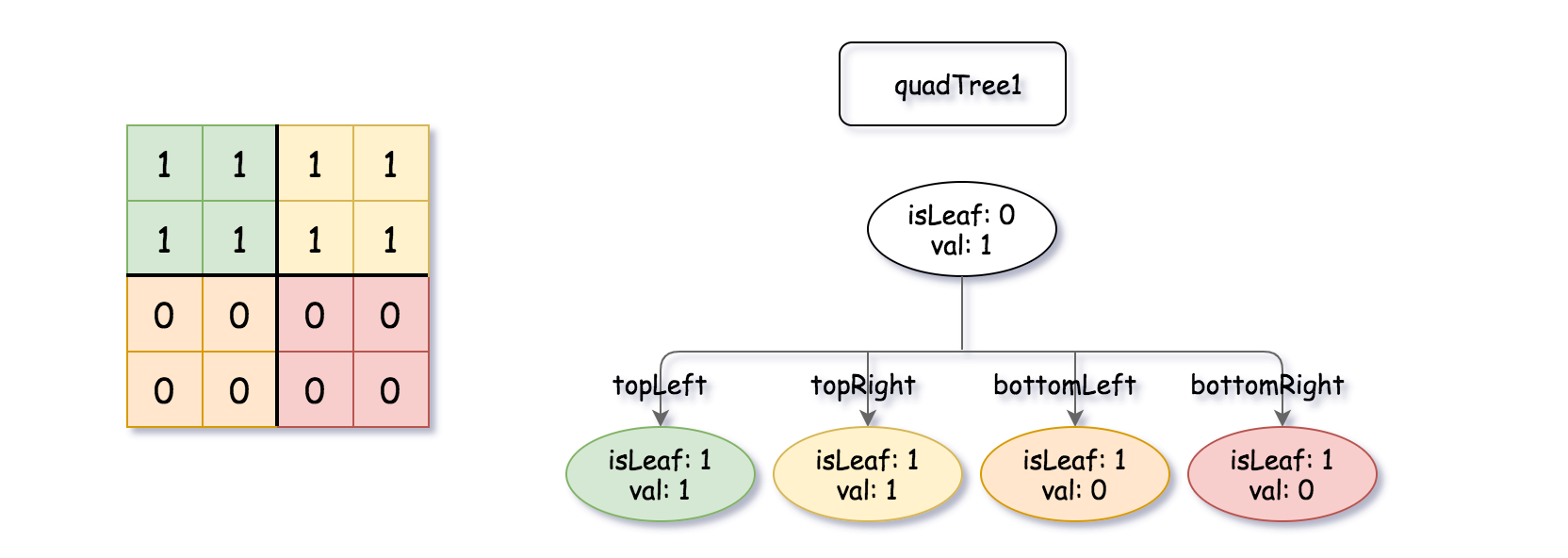
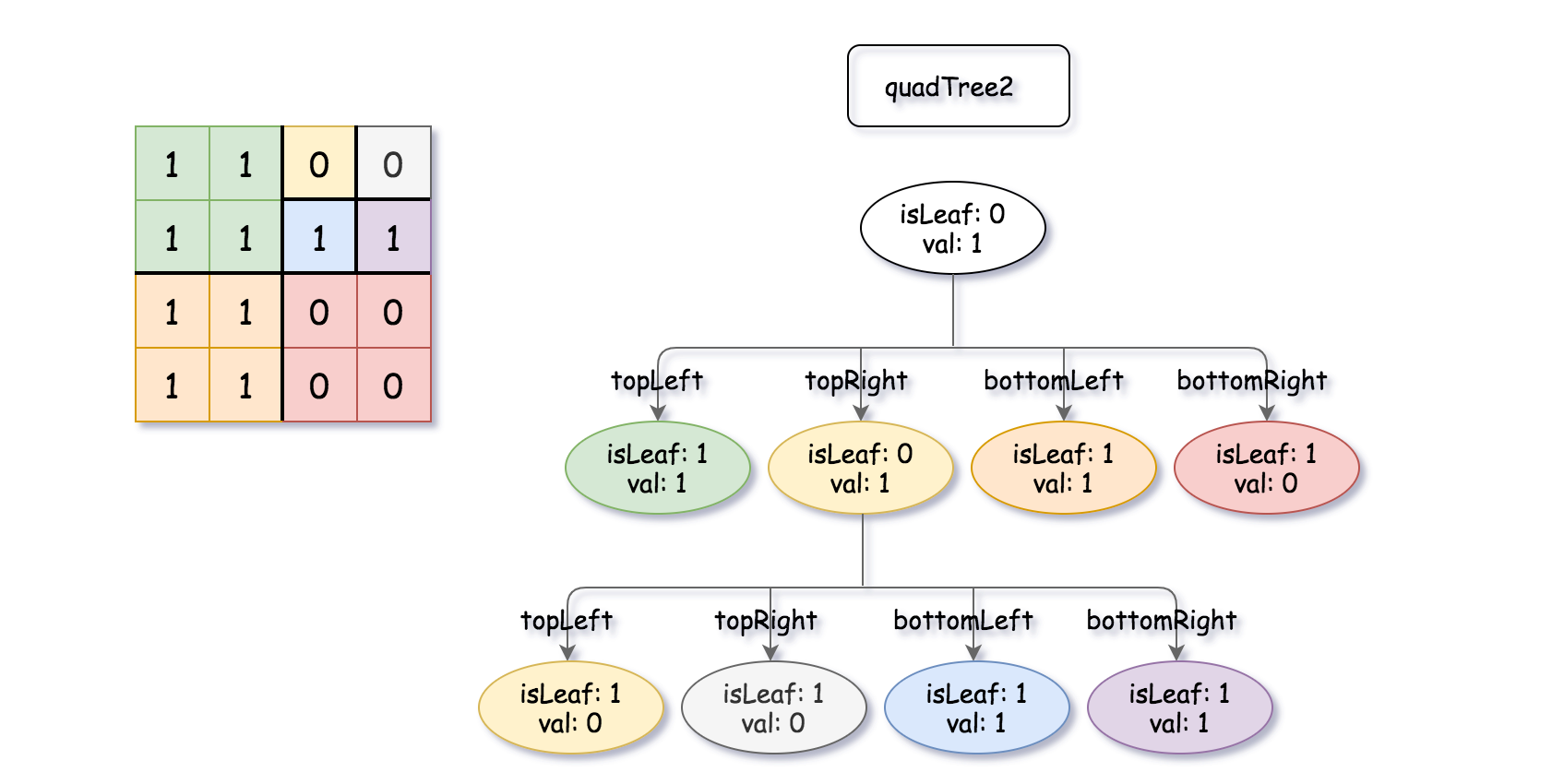
Input: quadTree1 = [[0,1],[1,1],[1,1],[1,0],[1,0]] , quadTree2 = [[0,1],[1,1],[0,1],[1,1],[1,0],null,null,null,null,[1,0],[1,0],[1,1],[1,1]] Output: [[0,0],[1,1],[1,1],[1,1],[1,0]] Explanation: quadTree1 and quadTree2 are shown above. You can see the binary matrix which is represented by each Quad-Tree. If we apply logical bitwise OR on the two binary matrices we get the binary matrix below which is represented by the result Quad-Tree. Notice that the binary matrices shown are only for illustration, you don't have to construct the binary matrix to get the result tree.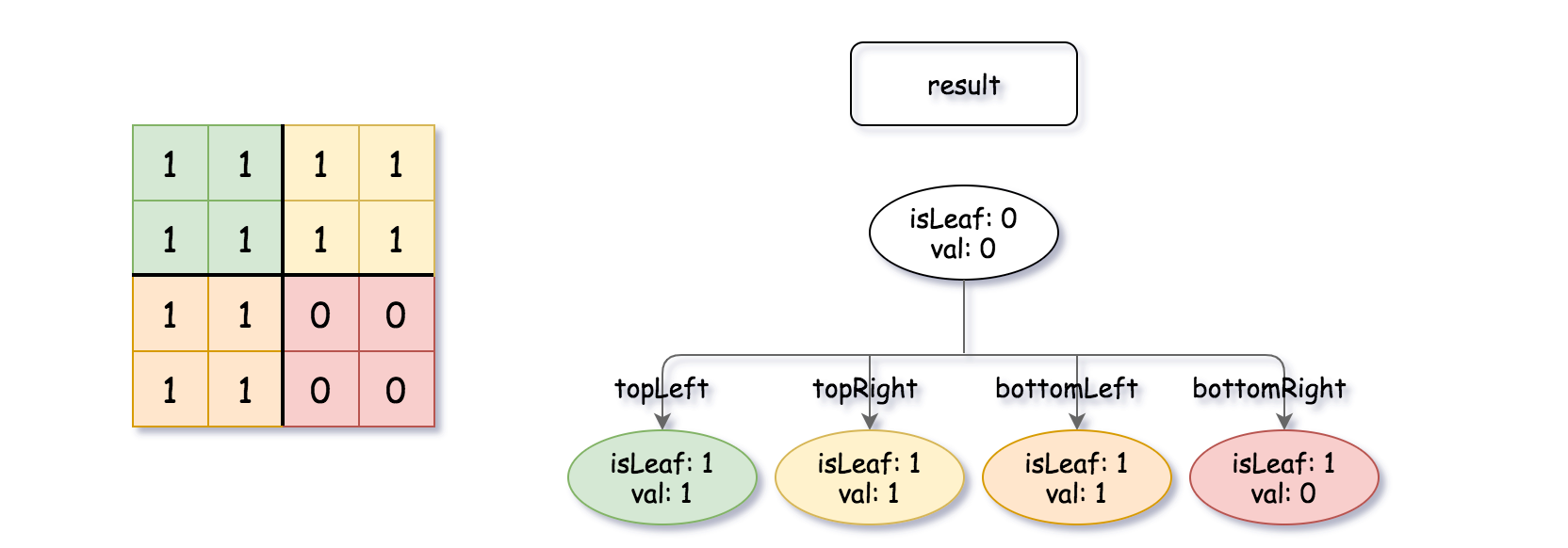
Example 2:
Input: quadTree1 = [[1,0]], quadTree2 = [[1,0]] Output: [[1,0]] Explanation: Each tree represents a binary matrix of size 1*1. Each matrix contains only zero. The resulting matrix is of size 1*1 with also zero.
Constraints:
quadTree1andquadTree2are both valid Quad-Trees each representing an * ngrid.n == 2xwhere0 <= x <= 9.
Solutions
-
/* // Definition for a QuadTree node. class Node { public boolean val; public boolean isLeaf; public Node topLeft; public Node topRight; public Node bottomLeft; public Node bottomRight; public Node() {} public Node(boolean _val,boolean _isLeaf,Node _topLeft,Node _topRight,Node _bottomLeft,Node _bottomRight) { val = _val; isLeaf = _isLeaf; topLeft = _topLeft; topRight = _topRight; bottomLeft = _bottomLeft; bottomRight = _bottomRight; } }; */ class Solution { public Node intersect(Node quadTree1, Node quadTree2) { return dfs(quadTree1, quadTree2); } private Node dfs(Node t1, Node t2) { if (t1.isLeaf && t2.isLeaf) { return new Node(t1.val || t2.val, true); } if (t1.isLeaf) { return t1.val ? t1 : t2; } if (t2.isLeaf) { return t2.val ? t2 : t1; } Node res = new Node(); res.topLeft = dfs(t1.topLeft, t2.topLeft); res.topRight = dfs(t1.topRight, t2.topRight); res.bottomLeft = dfs(t1.bottomLeft, t2.bottomLeft); res.bottomRight = dfs(t1.bottomRight, t2.bottomRight); boolean isLeaf = res.topLeft.isLeaf && res.topRight.isLeaf && res.bottomLeft.isLeaf && res.bottomRight.isLeaf; boolean sameVal = res.topLeft.val == res.topRight.val && res.topRight.val == res.bottomLeft.val && res.bottomLeft.val == res.bottomRight.val; if (isLeaf && sameVal) { res = res.topLeft; } return res; } } -
/* // Definition for a QuadTree node. class Node { public: bool val; bool isLeaf; Node* topLeft; Node* topRight; Node* bottomLeft; Node* bottomRight; Node() { val = false; isLeaf = false; topLeft = NULL; topRight = NULL; bottomLeft = NULL; bottomRight = NULL; } Node(bool _val, bool _isLeaf) { val = _val; isLeaf = _isLeaf; topLeft = NULL; topRight = NULL; bottomLeft = NULL; bottomRight = NULL; } Node(bool _val, bool _isLeaf, Node* _topLeft, Node* _topRight, Node* _bottomLeft, Node* _bottomRight) { val = _val; isLeaf = _isLeaf; topLeft = _topLeft; topRight = _topRight; bottomLeft = _bottomLeft; bottomRight = _bottomRight; } }; */ class Solution { public: Node* intersect(Node* quadTree1, Node* quadTree2) { return dfs(quadTree1, quadTree2); } Node* dfs(Node* t1, Node* t2) { if (t1->isLeaf && t2->isLeaf) return new Node(t1->val || t2->val, true); if (t1->isLeaf) return t1->val ? t1 : t2; if (t2->isLeaf) return t2->val ? t2 : t1; Node* res = new Node(); res->topLeft = dfs(t1->topLeft, t2->topLeft); res->topRight = dfs(t1->topRight, t2->topRight); res->bottomLeft = dfs(t1->bottomLeft, t2->bottomLeft); res->bottomRight = dfs(t1->bottomRight, t2->bottomRight); bool isLeaf = res->topLeft->isLeaf && res->topRight->isLeaf && res->bottomLeft->isLeaf && res->bottomRight->isLeaf; bool sameVal = res->topLeft->val == res->topRight->val && res->topRight->val == res->bottomLeft->val && res->bottomLeft->val == res->bottomRight->val; if (isLeaf && sameVal) res = res->topLeft; return res; } }; -
""" # Definition for a QuadTree node. class Node: def __init__(self, val, isLeaf, topLeft, topRight, bottomLeft, bottomRight): self.val = val self.isLeaf = isLeaf self.topLeft = topLeft self.topRight = topRight self.bottomLeft = bottomLeft self.bottomRight = bottomRight """ class Solution: def intersect(self, quadTree1: "Node", quadTree2: "Node") -> "Node": def dfs(t1, t2): if t1.isLeaf and t2.isLeaf: return Node(t1.val or t2.val, True) if t1.isLeaf: return t1 if t1.val else t2 if t2.isLeaf: return t2 if t2.val else t1 res = Node() res.topLeft = dfs(t1.topLeft, t2.topLeft) res.topRight = dfs(t1.topRight, t2.topRight) res.bottomLeft = dfs(t1.bottomLeft, t2.bottomLeft) res.bottomRight = dfs(t1.bottomRight, t2.bottomRight) isLeaf = ( res.topLeft.isLeaf and res.topRight.isLeaf and res.bottomLeft.isLeaf and res.bottomRight.isLeaf ) sameVal = ( res.topLeft.val == res.topRight.val == res.bottomLeft.val == res.bottomRight.val ) if isLeaf and sameVal: res = res.topLeft return res return dfs(quadTree1, quadTree2) -
/** * Definition for a QuadTree node. * type Node struct { * Val bool * IsLeaf bool * TopLeft *Node * TopRight *Node * BottomLeft *Node * BottomRight *Node * } */ func intersect(quadTree1 *Node, quadTree2 *Node) *Node { var dfs func(*Node, *Node) *Node dfs = func(t1, t2 *Node) *Node { if t1.IsLeaf && t2.IsLeaf { return &Node{Val: t1.Val || t2.Val, IsLeaf: true} } if t1.IsLeaf { if t1.Val { return t1 } return t2 } if t2.IsLeaf { if t2.Val { return t2 } return t1 } res := &Node{} res.TopLeft = dfs(t1.TopLeft, t2.TopLeft) res.TopRight = dfs(t1.TopRight, t2.TopRight) res.BottomLeft = dfs(t1.BottomLeft, t2.BottomLeft) res.BottomRight = dfs(t1.BottomRight, t2.BottomRight) isLeaf := res.TopLeft.IsLeaf && res.TopRight.IsLeaf && res.BottomLeft.IsLeaf && res.BottomRight.IsLeaf sameVal := res.TopLeft.Val == res.TopRight.Val && res.TopRight.Val == res.BottomLeft.Val && res.BottomLeft.Val == res.BottomRight.Val if isLeaf && sameVal { res = res.TopLeft } return res } return dfs(quadTree1, quadTree2) }