Welcome to Subscribe On Youtube

547. Number of Provinces

Description

There are n cities. Some of them are connected, while some are not. If city a is connected directly with city b, and city b is connected directly with city c, then city a is connected indirectly with city c.

A province is a group of directly or indirectly connected cities and no other cities outside of the group.

You are given an n x n matrix isConnected where isConnected[i][j] = 1 if the ith city and the jth city are directly connected, and isConnected[i][j] = 0 otherwise.

Return the total number of provinces.

 

Example 1:

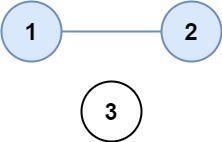
Input: isConnected = [[1,1,0],[1,1,0],[0,0,1]]
Output: 2

Example 2:

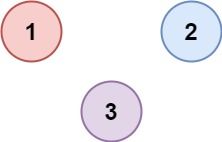
Input: isConnected = [[1,0,0],[0,1,0],[0,0,1]]
Output: 3

 

Constraints:

• 1 <= n <= 200
• n == isConnected.length
• n == isConnected[i].length
• isConnected[i][j] is 1 or 0.
• isConnected[i][i] == 1
• isConnected[i][j] == isConnected[j][i]

Solutions

• Java
• C++
• Python
• Go
• TypeScript
• RenderScript

• class Solution {
      private int[][] g;
      private boolean[] vis;
  
      public int findCircleNum(int[][] isConnected) {
          g = isConnected;
          int n = g.length;
          vis = new boolean[n];
          int ans = 0;
          for (int i = 0; i < n; ++i) {
              if (!vis[i]) {
                  dfs(i);
                  ++ans;
              }
          }
          return ans;
      }
  
      private void dfs(int i) {
          vis[i] = true;
          for (int j = 0; j < g.length; ++j) {
              if (!vis[j] && g[i][j] == 1) {
                  dfs(j);
              }
          }
      }
  }
  

• class Solution {
  public:
      int findCircleNum(vector<vector<int>>& isConnected) {
          int n = isConnected.size();
          int ans = 0;
          bool vis[n];
          memset(vis, false, sizeof(vis));
          function<void(int)> dfs = [&](int i) {
              vis[i] = true;
              for (int j = 0; j < n; ++j) {
                  if (!vis[j] && isConnected[i][j]) {
                      dfs(j);
                  }
              }
          };
          for (int i = 0; i < n; ++i) {
              if (!vis[i]) {
                  dfs(i);
                  ++ans;
              }
          }
          return ans;
      }
  };
  

• class Solution:
      def findCircleNum(self, isConnected: List[List[int]]) -> int:
          def dfs(i: int):
              vis[i] = True
              for j, x in enumerate(isConnected[i]):
                  if not vis[j] and x:
                      dfs(j)
  
          n = len(isConnected)
          vis = [False] * n
          ans = 0
          for i in range(n):
              if not vis[i]:
                  dfs(i)
                  ans += 1
          return ans
  
  

• func findCircleNum(isConnected [][]int) (ans int) {
  	n := len(isConnected)
  	vis := make([]bool, n)
  	var dfs func(int)
  	dfs = func(i int) {
  		vis[i] = true
  		for j, x := range isConnected[i] {
  			if !vis[j] && x == 1 {
  				dfs(j)
  			}
  		}
  	}
  	for i, v := range vis {
  		if !v {
  			ans++
  			dfs(i)
  		}
  	}
  	return
  }
  

• function findCircleNum(isConnected: number[][]): number {
      const n = isConnected.length;
      const vis: boolean[] = new Array(n).fill(false);
      const dfs = (i: number) => {
          vis[i] = true;
          for (let j = 0; j < n; ++j) {
              if (!vis[j] && isConnected[i][j]) {
                  dfs(j);
              }
          }
      };
      let ans = 0;
      for (let i = 0; i < n; ++i) {
          if (!vis[i]) {
              dfs(i);
              ++ans;
          }
      }
      return ans;
  }
  
  

• impl Solution {
      fn dfs(is_connected: &mut Vec<Vec<i32>>, vis: &mut Vec<bool>, i: usize) {
          vis[i] = true;
          for j in 0..is_connected.len() {
              if vis[j] || is_connected[i][j] == 0 {
                  continue;
              }
              Self::dfs(is_connected, vis, j);
          }
      }
  
      pub fn find_circle_num(mut is_connected: Vec<Vec<i32>>) -> i32 {
          let n = is_connected.len();
          let mut vis = vec![false; n];
          let mut res = 0;
          for i in 0..n {
              if vis[i] {
                  continue;
              }
              res += 1;
              Self::dfs(&mut is_connected, &mut vis, i);
          }
          res
      }
  }
  
  

All Problems

All Solutions